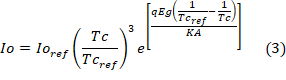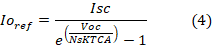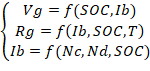http://dx.doi.org/10.35381/r.k.v5i2.960
Modelado, diseño y simulación de sistemas de micro-generación solar fotovoltaicos utilizando MATLAB
Modeling, design and simulation of photovoltaic solar micro-generation systems using MATLAB
Marcos A. Ponce-Jara
Universidad Laica Eloy Alfaro de Manabí
Ecuador
https://orcid.org/0000-0002-4450-4740
Jaime E. Chancay-Castro
Universidad Laica Eloy Alfaro de Manabí
Ecuador
https://orcid.org/0000-0002-5473-6094
Carlos Velásquez-Figueroa
Universidad Laica Eloy Alfaro de Manabí
Ecuador
https://orcid.org/0000-0003-0931-4914
Giselle Velásquez-Figueroa
giselle.velasquez@uleam.edu.ec
Universidad Laica Eloy Alfaro de Manabí
Ecuador
https://orcid.org/0000-0002-4494-6784
Recepción: 02 de junio 2020
Revisado: 24 de julio 2020
Aprobación: 17 de agosto 2020
Publicación: 01 de septiembre 2020
RESUMEN
La investigación tuvo por objetivo realizar un modelado, diseño y simulación de sistemas de micro-generación solar fotovoltaicos utilizando MATLAB como aporte de la Universidad Laica Eloy Alfaro de Manabí, a la conformación de alternativas energéticas viables en beneficio de la población ecuatoriana. Se desarrolló en función del enfoque cuantitativo, tipo descriptivo con apoyo de modalidad proyecto factible, se procedió a construir el modelado, diseño y simulación, el cual se presenta en una fase descriptiva matemática y otra de simulación, desplegadas en el apartado de propuesta tecnológica. Mediante el estudio por separado de cada elemento del sistema solar fotovoltaico aislado, se ha profundizado en su comportamiento dinámico. Además, ha permitido el diseño de una herramienta o aplicación parametrizable según las características técnicas de cada elemento del sistema, permitiendo simular sistemas solar fotovoltaicos incorporando datos reales de radicación solar y temperatura del sitio físico donde se realiza el estudio.
Descriptores: Energía solar; fuente de energía renovable; ingeniería de la energía solar; electricidad. (Palabras tomadas del Tesauro UNESCO).
ABSTRACT
The objective of the research was to carry out a modeling, design and simulation of photovoltaic solar micro-generation systems using MATLAB as a contribution from the Universidad Laica Eloy Alfaro de Manabí, to the formation of viable energy alternatives for the benefit of the Ecuadorian population. It was developed based on the quantitative approach, descriptive type supported by the feasible project modality, the modeling, design and simulation were built, which is presented in a mathematical descriptive phase and a simulation phase, displayed in the technological proposal section. By separately studying each element of the isolated photovoltaic solar system, its dynamic behavior has been deepened. In addition, it has allowed the design of a parameterizable tool or application according to the technical characteristics of each element of the system, allowing the simulation of photovoltaic solar systems incorporating real data on solar radiation and temperature of the physical site where the study is carried out.
Descriptors: Solar energy; renewable energy sources; solar power engineering; electricity. (Words taken from the UNESCO Thesaurus).
INTRODUCCIÓN
La calidad de vida de las personas en un mundo globalizado, se ve cada vez más comprometida para las clases sociales medias y pobres, sobre todo en los países llamados en vía de desarrollo, por cuanto la generación de electricidad tradicional, requiere de grandes inversiones para llegar a todos los rincones de la nación, aunado a la escasa cultura de pago por parte de los usuarios en proporción salario/servicios, a juicio de (Ffrench-Davis, 2017), esta postura obliga el ingreso de los países a la llamada “economía internacional de mercado”, sumado a la era de la sustentabilidad y sostenibilidad (Cortés-Mura & Peña-Reyes, 2015).
Una alternativa viable para la generación de electricidad a bajo costo en el mediano – largo plazo, así como mínimo impacto ambiental – ecológico, beneficia a las familias, pequeños productores rurales, a tener el servicio eléctrico para elevar su productividad y calidad de vida (Ovalle-Cubillos, 2014). Siendo necesario ubicar alternativas de micro-generación solar fotovoltaicos, por cuanto esto contribuye a proporcionar energía eléctrica en las condiciones antes descritas.
En el Ecuador a juicio de (Muñoz-Vizhñay, et al., 2018), la generación solar fotovoltaicos, es factible por condiciones climáticas, capacidad tecnológica para la instalación, ahorro al consumidor en el largo plazo, siendo considerable educar a la población, sobre los beneficios integrales que brinda este tipo de alternativa eléctrica, siendo posible para tal fin, que las instituciones de educación universitaria, se involucren en proyectos pilotos para evidenciar las bondades energéticas, ambientales, sobre todo cuando (Cisterna-Arellano, et al., 2020), advierten que esta inversión sin presencia del Estado, no resulta rentable como iniciativa privada, siendo necesaria diseñar políticas que permitan el impulso de este tipo de iniciativas sustentables (Lockwood, et al., 2017).
Sin embargo, en donde se han desarrollado proyectos pilotos de sustitución de generación eléctrica tradicional por alternativa, ha resultado favorable para la organización receptora, tal como se evidencia en la experiencia de (Pérez-Parada, et al., 2017), otra investigación similar es la presentada por (Pereira-Micena, et al., 2018), quienes exponen las bondades de contar con sistemas alternativos de energía para la movilización de los procesos productivos realizados por el ser humano, constituyéndose en una viable opción, siendo pertinente focalizar políticas claras de apoyo a este tipo de emprendimiento, tanto en lo legal como financiero.
Siendo una tarea indispensable de las universidades ecuatorianas, generar alternativas viables para potenciar la posibilidad de promover una cultura energética, basada en lo sustentable, siendo primordial en una primera fase de investigación, realizar simulación matemática con la finalidad de establecer una planificación estratégica sobre la factibilidad de consolidar exitosamente este tipo de iniciativas, tal como recomiendan (Vera-Dávila, et al., 2018), siendo considerable desarrollar los cálculos matemáticos a través de MATLAB, por cuanto esta permite diseñar con precisión el modelado (Moreno, 2017).
En función de lo planteado, se presentan los modelos matemáticos utilizados en el desarrollo de la herramienta de simulación parametrizable “App Microgeneración Solar Fotovoltaica Uleam” desarrolladas a través del software MATLAB. Adicionalmente, se presentan las simulaciones de validación, puesta en marcha y uso de los datos de radiación solar tomados por la estación meteorológica Automática de la Universidad Laica Eloy Alfaro de Manabí; esta estación forma parte del proyecto de investigación “Análisis de los recursos energéticos en los cantones Manta, Montecristi y Jaramijó con fines de generación eléctrica”.
Por consiguiente, la investigación tuvo por objetivo realizar un modelado, diseño y simulación de sistemas de micro-generación solar fotovoltaicos utilizando MATLAB como aporte de la Universidad Laica Eloy Alfaro de Manabí, a la conformación de alternativas energéticas viables en beneficio de la población ecuatoriana.
MÉTODO
La propuesta investigativa se desarrolló en función del enfoque cuantitativo, tipo descriptivo con apoyo de modalidad proyecto factible (Palella & Martins, 2015, p. 97), de ese modo, se procedió a construir el modelado, diseño y simulación, el cual se presenta en una fase descriptiva matemática y otra de simulación, desplegadas en el apartado de propuesta tecnológica.
PROPUESTA TECNOLÓGICA
Sistema solar fotovoltaico
Según (, et al., 2019), un sistema fotovoltaico es un conjunto de dispositivos que, a partir de la insolación o radiación solar, produce energía eléctrica, la almacenan y la tratan hasta tenerlas en condiciones nominales para ser aprovechada por el hombre. La figura 1 muestra un típico sistema solar fotovoltaico operando de forma aislada, el cual se toma como referencia para la construcción del modelo matemático presentado en este artículo.
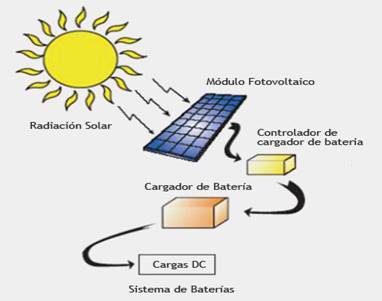
Figura 1. Sistema solar fotovoltaico autónomo regulado con inversor, aislado de red. Fuente: Carmona (2018).
Modelos matemáticos y MATLAB
Un modelo matemático es un tipo de modelo científico que emplea el formulismo matemático. Para modelar matemáticamente sistemas eléctricos por lo general se lo realiza a partir de modelos circuitales equivalentes, a partir del cual se calcula o reproduce su comportamiento en función del tiempo. Actualmente el uso de software especializados permite trasladar estos modelos a un ambiente digital para realizar simulaciones con el fin de evaluar y analizar su comportamiento de una manera más fácil y didáctica (Poznyak, 2005).
El software MATLAB es uno de los más utilizados tanto en la academia como en la industria debido a sus características avanzadas en el tratamiento de datos. Mediante el uso de su herramienta SIMULINK es posible crear representaciones visuales de los dispositivos o sistemas modelados matemáticamente (Cruz, 2016). Es por esto que se ha escogido como herramienta de trabajo para el propósito perseguido en este artículo.
Panel solar
Una celda solar fotovoltaica se puede
modelarse a partir de la figura 2. Este circuito equivalente consta de: 1)
fuente ![]() que
emula la corriente fotogenerada (depende de la radiación solar); 2) diodo de
unión p-n, que por medio del efecto fotoeléctrico convierte la radiación solar
en energía eléctrica; y 3) elementos resistivos que emulan las pérdidas del
sistema
que
emula la corriente fotogenerada (depende de la radiación solar); 2) diodo de
unión p-n, que por medio del efecto fotoeléctrico convierte la radiación solar
en energía eléctrica; y 3) elementos resistivos que emulan las pérdidas del
sistema ![]() (perdidas
por corriente de fuga, o resistencia
(perdidas
por corriente de fuga, o resistencia ![]() )
y la resistencia
)
y la resistencia ![]() (caída
de tensión a la salida o resistencia
(caída
de tensión a la salida o resistencia ![]() ),
estos valores idealmente se consideran
),
estos valores idealmente se consideran ![]() y
y
![]() para
obtener los valores máximos de corriente del circuito (Vera-Dávila,
et al., 2018).
para
obtener los valores máximos de corriente del circuito (Vera-Dávila,
et al., 2018).
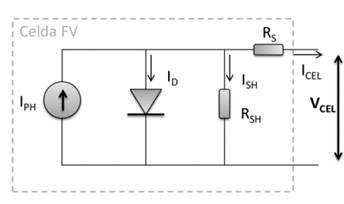
Figura 2. Circuito Equivalente para el modelado de un panel solar.
Fuente: Vera-Dávila, et al. (2018).
La ecuación (1) describe la corriente generada por la célula solar de la figura 2:
![]()
Sustituyendo las variables ![]() de (1) por su modelo matemático, se obtiene:
de (1) por su modelo matemático, se obtiene:
![]()
Donde:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dentro de esta fórmula, la corriente de
saturación inversa del diodo depende también de la temperatura y de una
corriente ![]() resultando
en:
resultando
en:
|
|
|
|
|
|
Donde:
Normalmente las celdas solares se producen
para valores de potencia y voltaje relativamente bajos (2W a 5V), por tanto,
para obtener la potencia deseada en cada panel, estas se agrupan en serie o
paralelo. Para conseguir esto, a la ecuación (2) se le agregan los coeficientes
![]() (número
de módulos en paralelo) y
(número
de módulos en paralelo) y ![]() (número
de celdas en serie), obteniendo la ecuación (5). Esta ecuación se puede
simplificar según la ecuación (6), debido a que la resistencia Shunt no afecta
de manera directa en la eficiencia de una celda solar, por considerarse
infinita
(número
de celdas en serie), obteniendo la ecuación (5). Esta ecuación se puede
simplificar según la ecuación (6), debido a que la resistencia Shunt no afecta
de manera directa en la eficiencia de una celda solar, por considerarse
infinita ![]() .
Por tanto, el modelado tanto de una como de varias células solares vendrá
determinada por (6).
.
Por tanto, el modelado tanto de una como de varias células solares vendrá
determinada por (6).
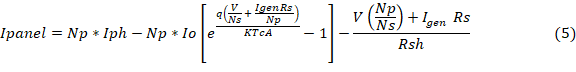
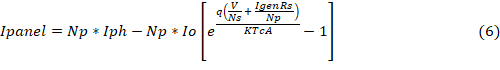
Regulador
Para modelar el sistema propuesto en la figura 1, se implementará un convertidor DC/DC y un regulador de carga para baterías. La implementación del convertidor DC/DC permite mejorar el rendimiento global del sistema fotovoltaico y realizar un control a diferentes niveles. El modelo matemático más sencillo del comportamiento de un regulador se fundamenta en un principio básico aplicado a los convertidores ya sean reductores (Buck) o elevadores (Boost) (Marulanda-Durango, et al., 2017). Por lo general, en convertidores DC/DC la potencia de entrada es igual a la potencia de salida más las perdidas por eficiencia o factor de trabajo, tal como muestran las fórmulas (7) y (8)
![]()
![]()
Por otro lado, el regulador
de carga tiene la función de proteger la carga de las baterías ante las
situaciones de riesgo más comunes, como son las sobrecargas y sobre descargas.
El modelo de este regulador se muestra en la figura 3; está formado relés
adaptados (controlados mediante
comparadores ![]() e
e
![]() ) para brindar una conexión y desconexión
del sistema, específicamente entre dos elementos: el panel solar y la carga
conectada.
) para brindar una conexión y desconexión
del sistema, específicamente entre dos elementos: el panel solar y la carga
conectada.
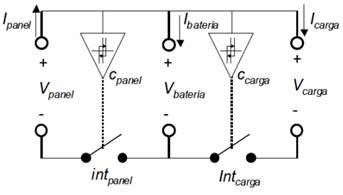
Figura 3. Circuito equivalente de un regulador de carga de la batería.
Fuente: Inguil-Lema & Ortega-Espinoza (2014).
A juicio de (Inguil-Lema & Ortega-Espinoza, 2014), las relaciones condicionadas de operación para un funcionamiento correcto del regulador son:
1. Cuando la batería entra en carga completa o sobrecarga, el controlador desconecta los paneles solares evitando la saturación de la batería.
![]()
Siendo, ![]() y
y
![]() el
umbral máximo y mínimo para la desconexión del panel.
el
umbral máximo y mínimo para la desconexión del panel.
2. Cuando la batería entra en carga agotada o sobredescarga, el controlador desconecta la carga evitando descargas profundas de la batería
![]()
Siendo, ![]() el
umbral límite para desconectar las cargas y
el
umbral límite para desconectar las cargas y ![]() el
umbral mínimo que tiene que superar la batería para permitir la conexión de una
carga.
el
umbral mínimo que tiene que superar la batería para permitir la conexión de una
carga.
Batería
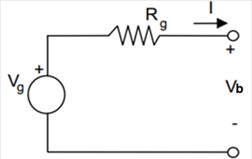
El modelo más básico de una batería es el que
se muestra en la figura 4. Se trata de una fuente de alimentación real con una
fuente de generación ![]() en
serie con una resistencia interna
en
serie con una resistencia interna ![]() y un voltaje en circuito abierto
y un voltaje en circuito abierto ![]() .
Las variables más importantes en la dinámica de una batería son: la corriente
que circula a través de la batería, la capacidad de almacenamiento de energía,
la temperatura de trabajo, el
.
Las variables más importantes en la dinámica de una batería son: la corriente
que circula a través de la batería, la capacidad de almacenamiento de energía,
la temperatura de trabajo, el ![]() o
estado de carga de la batería y los coeficientes de trabajo para las etapas de
carga y descarga.
o
estado de carga de la batería y los coeficientes de trabajo para las etapas de
carga y descarga.
|
|
|
Figura 4. Circuito equivalente de una batería.
Fuente: Murillo (2003).
Aplicando las leyes de Kirchhoff al circuito se obtienen las ecuaciones (11) y (12):
![]()
![]()
Estas ecuaciones no son suficientes para
modelar el comportamiento y dinámica de una batería. Una solución consiste en
considerar la variable ![]() (ver
(13)) como indicador de la energía almacenada para modelar de forma efectiva el
comportamiento de este dispositivo (Murillo, 2003).
(ver
(13)) como indicador de la energía almacenada para modelar de forma efectiva el
comportamiento de este dispositivo (Murillo, 2003).
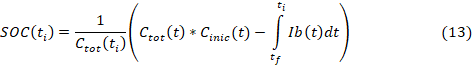
![]()
Donde:
|
|
|
|
|
|
|
|
|
|
|
|
Inversor
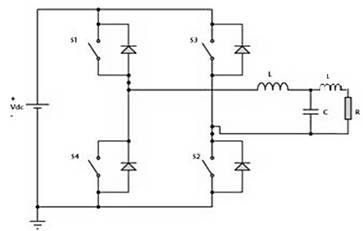
Los sistemas solares fotovoltaicos son capaces también de subministrar energía a cargas AC mediante el uso de un inversor de corriente DC/AC (ver figura 5). Para este trabajo se consideró modelar un inversor monofásico de puente completo. Estos inversores, cuentan con 3 etapas que son: 1) Control PWM para H-Bridge; 2) Puente inversor completo (tipo H); y 3) Filtrado de la onda (Filtro). Las características y funcionalidades de este dispositivo se detallan a continuación:
1) Posee cuatro interruptores o dispositivos de conmutación de potencia (transistores IGBT), conectados en antiparalelo con un diodo.
2) Convierte la corriente continua en alterna, bajo el principio de que la corriente positiva y negativa que circula es controlada por los dispositivos de conmutación y los diodos de descarga en antiparalelo sirven de protección.
3)
 |
Se debe contemplar la excitación de la
Figura 5. Circuito equivalente eléctrico de un inversor de puente completo CC/AC con filtro LCL.
Fuente: Elaboración propia.
Para el control de los IGBT se usará el
control por modulación o ancho de pulsos PWM ![]() . esta es una técnica
de control cuyo objetivo es modificar el ciclo de trabajo de una señal
periódica, mediante la conmutación o conducción controlada de los dispositivos
conmutadores (IGBT) obteniéndose una onda sinusoidal de forma cuadrada; esta
onda se somete a una etapa final de filtrado (LCL) para obtener una señal
sinusoidal suavizada y con las mismas características que la de la red
eléctrica (Luna-Merino, 2010).
. esta es una técnica
de control cuyo objetivo es modificar el ciclo de trabajo de una señal
periódica, mediante la conmutación o conducción controlada de los dispositivos
conmutadores (IGBT) obteniéndose una onda sinusoidal de forma cuadrada; esta
onda se somete a una etapa final de filtrado (LCL) para obtener una señal
sinusoidal suavizada y con las mismas características que la de la red
eléctrica (Luna-Merino, 2010).
Cargas
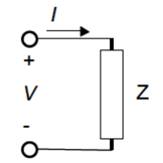 |
Para el modelado de la carga se toma como base los fundamentos matemáticos de las leyes eléctricas de Ohm (I=V/Z) y Watt (I=P/V) a partir del su circuito equivalente que se muestra en la figura 6, estas leyes se aplican tanto para las cargas que son conectadas en corriente continua o corriente alterna, en donde se obtienen los resultados partir de los valores nominales de impedancia o potencia propia.
Figura 6. Circuito equivalente básico de una carga (Impedancia Z).
Fuente: Murillo (2003).
Simulaciones
Para realizar todas las simulaciones se tomaron los datos de radiación y temperatura de la estación meteorológica de la Universidad Laica Eloy Alfaro de Manabí. Particularmente del día 19 de enero del 2020 (00:00h a 23:30h); estos datos se observan en la figura 7.
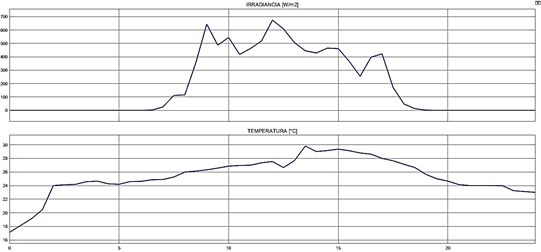
Figura 7. Lectura de radiación y temperatura de la ciudad de Manta día 20 de enero del 2020 en 24 horas.
Fuente: Estación meteorológica ULEAM.
Simulación Panel solar.
Para la simulación del panel solar en Matlab, se toma como referencia las características eléctricas y de un módulo de panel solar, modelo 1STH-215-P de la marca SOLTECH. Está formado por un arreglo de 60 células policristalinas por modulo. Los datos más relevantes extraídos de la ficha técnica son (HUB, 2017):
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
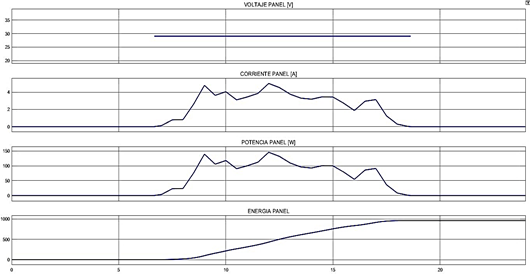 |
Una vez introducidos estos datos en el modelo matemático, se obtienen los resultados mostrados en la figura 8, donde se observan los valores de corriente, voltaje, potencia y energía producida durante 24 horas.
Figura 8. Comportamiento de un panel solar en 24 horas.
Fuente: Elaboración propia.
En estas graficas se puede verificar el
correcto funcionamiento del modelo matemático de 1 panel solar fotovoltaico.
Por un lado, se puede observar el ![]() ,
el cual corresponde con el dato proporcionado por el fabricante
,
el cual corresponde con el dato proporcionado por el fabricante ![]() . Por otro lado, se
observa la corriente generada por el panel solar, la cual depende de
. Por otro lado, se
observa la corriente generada por el panel solar, la cual depende de ![]() así como de la
radiación incidente; de hecho, si comparamos la gráfica de corriente generada
del panel con la gráfica de radiación (figura 7), se observa claramente que la
forma de corriente es muy parecida a esta. Haciendo el mismo análisis y
teniendo en cuenta que la tensión de trabajo es constante, se observa que la
potencia generada posee la misma forma que la corriente. Para poder simular una
instalación solar fotovoltaica de más de un panel solar fotovoltaico se propone
un sistema denominado
así como de la
radiación incidente; de hecho, si comparamos la gráfica de corriente generada
del panel con la gráfica de radiación (figura 7), se observa claramente que la
forma de corriente es muy parecida a esta. Haciendo el mismo análisis y
teniendo en cuenta que la tensión de trabajo es constante, se observa que la
potencia generada posee la misma forma que la corriente. Para poder simular una
instalación solar fotovoltaica de más de un panel solar fotovoltaico se propone
un sistema denominado ![]() (figura
9) donde se puede especificar el número de paneles en serie
(figura
9) donde se puede especificar el número de paneles en serie ![]() y
paralelo
y
paralelo ![]() que queremos conectar. El
funcionamiento sería exactamente el mismo.
que queremos conectar. El
funcionamiento sería exactamente el mismo.
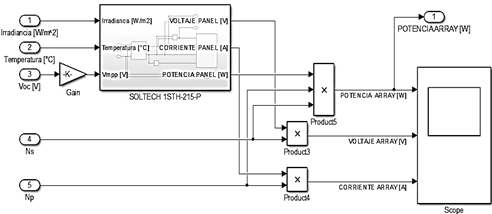
Figura 9. Modelo de un arreglo de paneles solares (PV ARRAY) en Matlab/Simulink.
Fuente: Elaboración propia.
Regulador
En este apartado se realiza la simulación
del convertidor DC/DC (función reductora) y del regulador de carga conectado a
la salida de la etapa de generación (![]() ); se simulan 2 paneles
conectados en paralelo. La
figura 10 muestra el modelo del convertidor DC/DC reductor. Para la simulación
de estos dispositivos se realizaron dos modelos según sea la aplicación:
); se simulan 2 paneles
conectados en paralelo. La
figura 10 muestra el modelo del convertidor DC/DC reductor. Para la simulación
de estos dispositivos se realizaron dos modelos según sea la aplicación:
1. Modelo en generación: el coeficiente de trabajo del convertidor se multiplica (figura 10).
2. Modelo en consumo o carga: el coeficiente de trabajo del convertidor se divide (modelo igual al de la figura 10 pero cambiando la multiplicación por una división).
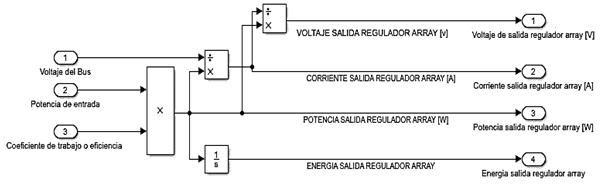
Figura 10. Modelo de convertidor DC/DC para el array de paneles en Matlab/Simulink. Fuente: Elaboración propia.
Como se muestra en la figura 1, el regulador
DC/DC está conectado entre los paneles y la batería, estableciendo de esta
manera un proceso de ![]() a
la salida de los paneles (valor de operación del bus (24V)), que permite
extraer los valores óptimos para un mejor funcionamiento tanto en la batería
como en el sistema.
a
la salida de los paneles (valor de operación del bus (24V)), que permite
extraer los valores óptimos para un mejor funcionamiento tanto en la batería
como en el sistema.
El modelo creado en SIMULINK consiste en un
control mediante el uso de comparadores de histéresis (![]() ,
el cual compara el
,
el cual compara el ![]() de
la batería (medido porcentualmente) con los umbrales máximo y mínimos
establecidos para controlar la apertura y cierre de los relés o interruptores.
de
la batería (medido porcentualmente) con los umbrales máximo y mínimos
establecidos para controlar la apertura y cierre de los relés o interruptores.
En la figura 11 se puede observar el comportamiento del convertidor DC/DC y en la figura 12 se observa el regulador de carga de la batería con sus bloques habilitadores y deshabilitadores de los paneles y la carga conectada al sistema y la programación condicional para el control de comparación por histéresis.
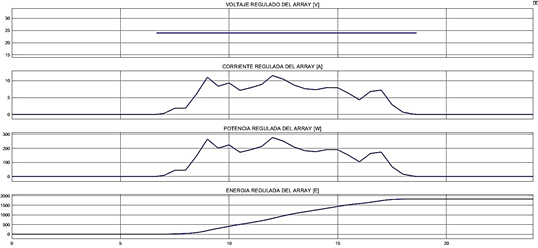
Figura 11. Convertidor DC/DC y visualización de los parámetros regulados del Array de paneles (24 voltios).
Fuente: Elaboración propia.
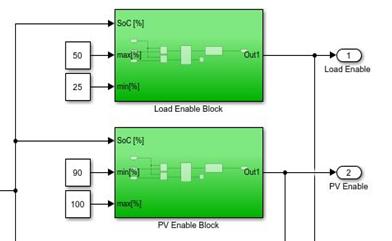
Figura 12. Control por histéresis mediante SoC (Regulador de carga de la batería) en Matlab/Simulink.
Fuente: Elaboración propia.
Los resultados de la validación de este
dispositivo, se muestran en el apartado de simulación de la batería, debido a
que para su funcionamiento es necesario tener la lectura del ![]() proveniente
del comportamiento del dispositivo de almacenamiento de energía.
proveniente
del comportamiento del dispositivo de almacenamiento de energía.
Batería
En este apartado se simula un banco de 4
baterías dispuesto de la siguiente manera: dos grupos de baterías conectados en
paralelo, donde cada grupo consta de dos baterías conectadas en serie. La
agrupación de barías en serie y paralelo se fundamenta, al igual que en el caso
de los paneles solares, mediante sus principios de asociación de dispositivos
(coeficientes o variables ![]() y
y ![]() ). El modelado de este
banco de baterías se realizó teniendo en cuenta las características técnicas de
la batería LVEG40-12 (12V-DC y 40A-h ) (ver Tabla 1) (BatterySolution, 2014). De esta manera se formó un banco de
baterías de 24V-DC y 80Ah de capacidad.
). El modelado de este
banco de baterías se realizó teniendo en cuenta las características técnicas de
la batería LVEG40-12 (12V-DC y 40A-h ) (ver Tabla 1) (BatterySolution, 2014). De esta manera se formó un banco de
baterías de 24V-DC y 80Ah de capacidad.
Tabla 1.
Características de la batería LVEG40-12.
|
|
|
|
|
|
|
|
|
Por otro lado, para esta simulación es
necesario realizar el modelado de la formula (13) SoC ![]() , mediante el cual se obtienen los valores de autonomía de la batería
permitiendo de esta manera realizar el control por histéresis que efectúa el
regulador de carga de la batería. La figura 13 muestra el modelado de SoC y la
figura 14 el modelo SIMULINK del banco de baterías.
, mediante el cual se obtienen los valores de autonomía de la batería
permitiendo de esta manera realizar el control por histéresis que efectúa el
regulador de carga de la batería. La figura 13 muestra el modelado de SoC y la
figura 14 el modelo SIMULINK del banco de baterías.
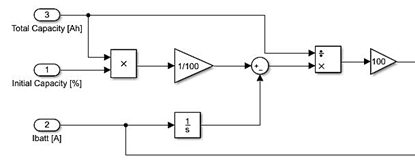
Figura 13. Ecuación para el cálculo del estado de carga de la batería ‘‘SoC’’ en MATLAB/SIMULINK. Fuente: Elaboración propia.
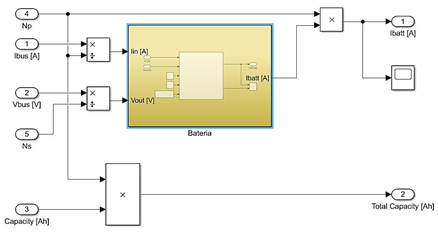
Figura 14. Modelo de un arreglo o banco de baterías en Matlab/Simulink. Fuente: Elaboración propia.
En la figura 15
se muestra el comportamiento del banco de baterías con regulador, conjuntamente
con los datos provenientes del apartado de ![]() . Además, se añade una carga de 300W a 24 V-DC desarrollada en el apartado del
. Además, se añade una carga de 300W a 24 V-DC desarrollada en el apartado del ![]() ”.
”.
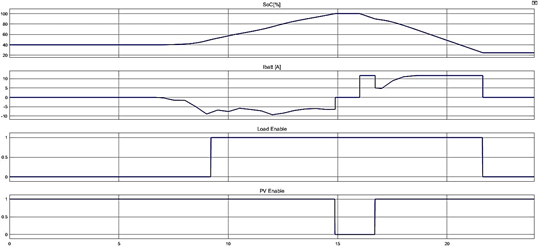
Figura 15. Lectura de datos
(V-I) y comportamiento del banco de baterías con regulador Fuente:
Elaboración propia.
La simulación que se presentan corresponde
a la evolución de la variable ![]() en su etapa de carga y descarga. Esta depende de la corriente que
circula por la batería, es decir la etapa en que la corriente es negativa
(absorbe energía proveniente de los paneles) (SoC-cargándose) y la etapa donde
la corriente es positiva (entrega la energía almacenada a la carga)
(SoC-descargándose). En las dos últimas gráficas se observa el comportamiento
del control
en su etapa de carga y descarga. Esta depende de la corriente que
circula por la batería, es decir la etapa en que la corriente es negativa
(absorbe energía proveniente de los paneles) (SoC-cargándose) y la etapa donde
la corriente es positiva (entrega la energía almacenada a la carga)
(SoC-descargándose). En las dos últimas gráficas se observa el comportamiento
del control ![]() , realizado por el regulador en función de la lectura de la energía
almacenada disponible o
, realizado por el regulador en función de la lectura de la energía
almacenada disponible o ![]() .
.
Inversor.
Se partió del modelado del circuito
eléctrico (figura 5) utilizando los modelos eléctricos equivalentes de SIMUINK,
estableciendo las 3 etapas que lo conforman: 1) ![]() de onda completa; 2)
de onda completa; 2) ![]() ; y 3) carga AC a la salida del inversor. Además, se añadió la etapa de
control PWM y el convertidor DC/DC conectado en etapa de consumo (ver figura
16).
; y 3) carga AC a la salida del inversor. Además, se añadió la etapa de
control PWM y el convertidor DC/DC conectado en etapa de consumo (ver figura
16).
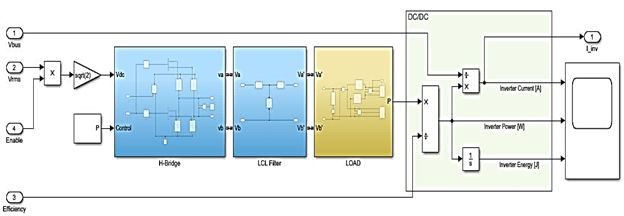
Figura 16. Etapas de la simulación del Inversor monofásico 24V-DC/155.56V-AC en Matlab/Simulink.
Fuente: Elaboración propia.
Una de las características principales del inversor es la conmutación controlada de los transistores del puente H para obtener una onda cuadrada alterna emulando la forma de onda sinusoidal como se muestra en la figura 17. Se observa un valor de voltaje pico de 155.56V-AC, entre fase y neutro.
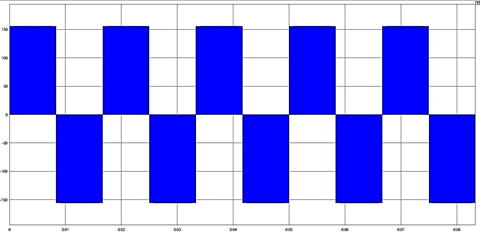
Figura 17. Onda cuadrada en AC a la salida del puente inversor controlado por PWM en Matlab/Simulink.
Fuente: Elaboración propia.
La forma de onda de la figura 17 se
introduce en del filtro ![]() para eliminar los componentes de alta frecuencia y obtener una onda
sinusoidal de 110V a 60Hz. Para poder simular estas formas de onda se conecta
una carga de 300W a 110 V-AC. La figura 18 muestra los valores obtenidos.
para eliminar los componentes de alta frecuencia y obtener una onda
sinusoidal de 110V a 60Hz. Para poder simular estas formas de onda se conecta
una carga de 300W a 110 V-AC. La figura 18 muestra los valores obtenidos.
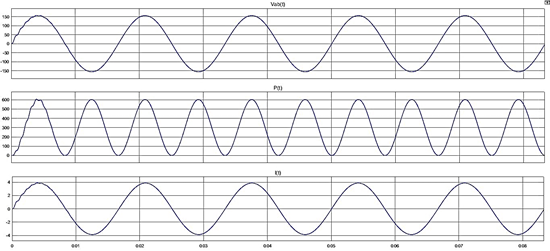
Figura 18. Onda sinusoidal filtrada (Filtro LCL), de una carga de 300W conectada en Matlab/Simulink.
Fuente: Elaboración propia.
Carga
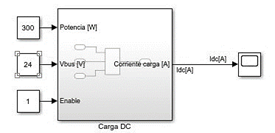
En este apartado se realizará la simulación y análisis de cargas en DC y AC, con el fin de presentar un análisis más exhaustivo del comportamiento de estas cuando se añaden al sistema. La simulación del comportamiento de una carga conectada en DC se observa en la figura 19.
|
|
|
Figura 19. Modelo de la carga DC en Matlab/Simulink.
Fuente: Elaboración propia.
Un sistema con una carga en AC, debido a
su naturaleza, es mucho más compleja que en DC; el comportamiento de esta
variará según el tipo de carga (inductiva, capacitiva o resistiva). Para
simular una carga en AC en el modelo propuesto y poder visualizar la señal
sinusoidal resultante se incorporan ![]() cuya la función es extraer de una onda sinusoidal los valores RMS de los
parámetros eléctricos. La figura 20 muestra el modelo en MISULINK y la figura
21 las formas de onda resultante con una resistencia de 40Ω.
cuya la función es extraer de una onda sinusoidal los valores RMS de los
parámetros eléctricos. La figura 20 muestra el modelo en MISULINK y la figura
21 las formas de onda resultante con una resistencia de 40Ω.
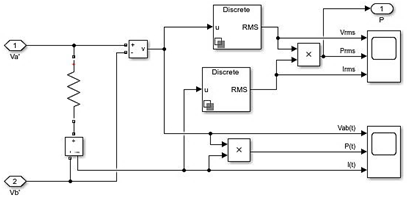
Figura 20. Modelado de la carga AC con bloques de medición RMS discretos en Matlab/Simulink.
Fuente: Elaboración propia.
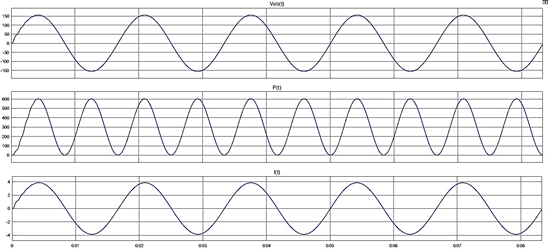 |
Figura 21. Lectura de voltaje, potencia y corriente (PICO A PICO) en la carga conectada de 40Ω AC.
Fuente: Elaboración propia.
Sistema solar fotovoltaico completo.
El sistema solar fotovoltaico aislado completo ha tomado en cuenta cada uno de los modelos explicados previamente para formar la estructura final. Como muestra la figura 23, este modelo se caracteriza por un bus de 24V que interconecta todos los dispositivos del sistema y que además entregará energía a las cargas en DC conectadas al mismo. En caso de existir una carga AC se incorpora un bus de 110V en corriente alterna para la conexión de este tipo de carga.
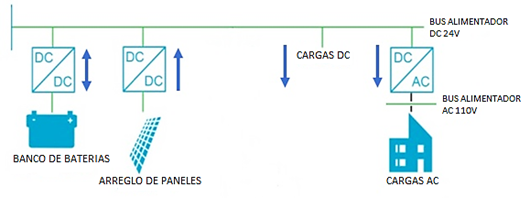
Figura 23. Arquitectura sistema solar fotovoltaico autónomo aislado para cargas DC - AC.
Fuente: Elaboración propia.
Sistema solar fotovoltaico autónomo aislado para cargas DC - AC.
Los modelos resultantes tanto para cargas en DC como en AC son los que se muestran en la figura 24 y 25. En cada uno de estos sistemas destacan tres etapas: 1) generación; 2) almacenamiento; y 3) consumo de carga. Es importante destacar que las simulaciones que obtengamos dependerán de las características técnicas de los paneles solares fotovoltaicos, baterías, inversor, además de las conexiones series o paralelo que se realice en los sistemas que se desea simular.
Por otro lado, al simular un sistema solar
fotovoltaico con cargas AC, debido a la complejidad de la simulación del
inversor (incorpora la apertura y cierre de transistores IGBT a una alta
frecuencia), se hace muy complejo simular el comportamiento de este por mucho
tiempo; esto se debe a un mayor uso de la CPU del computador, traduciéndose en
simulaciones con tiempos de espera muy largos dependiendo del rango de tiempo y
los datos que se estén procesando. Por este motivo para poder simular y validar
este tipo de sistemas se procedió a realizar un escalado de tiempo con la
finalidad de estudiar el comportamiento dinámico del sistema sin comprometer el
tiempo de espera. El escalado de tiempo se calculó según la formula (15):![]()
![]()
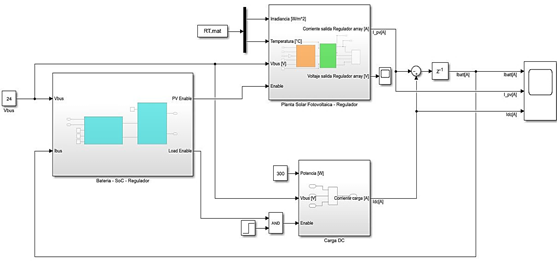
Figura 24. Modelo del sistema solar fotovoltaico autónomo aislado para cargas DC en Matlab/Simulink.
Fuente: Elaboración propia.
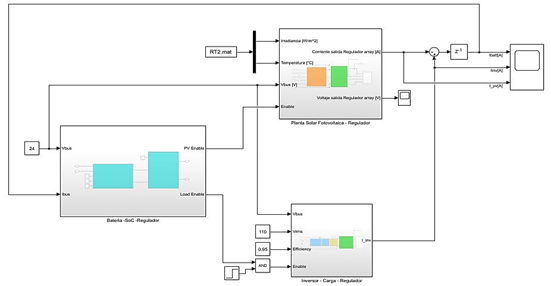 |
Figura 25. Modelo del sistema solar fotovoltaico autónomo aislado para cargas AC en Matlab/Simulink.
Fuente: Elaboración propia.
App-Microgeneración Solar Fotovoltaica.
La aplicación ![]() se
creaa mediante la interfaz gráfica
de usuario (GUI), para permitir agrupar y facilitar el manejo de todos los
programas o simulaciones parametrizables que fueron anteriormente creados y
analizados; evitando la presencia o el acceso a las carpetas raíz que contienen
los numerosos archivos que permiten funcionar a los programas correctamente y
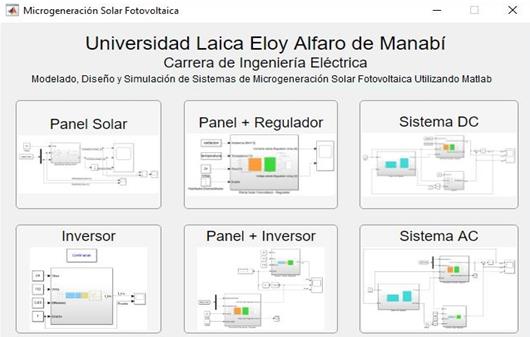
que pueden conducir a la confusión. La figura 26 muestra el diseño final de la
aplicación, a través de la cual se puede acceder a la simulación de cualquier
parte del sistema dando un clic en la parte que interese. Este es un entorno multitarea con simulaciones paralelas e
independientes, cuadros de textos de ayudas interactivas, interfaz de rápido
acceso e intuitiva que integra todos los modelos
se
creaa mediante la interfaz gráfica
de usuario (GUI), para permitir agrupar y facilitar el manejo de todos los
programas o simulaciones parametrizables que fueron anteriormente creados y
analizados; evitando la presencia o el acceso a las carpetas raíz que contienen
los numerosos archivos que permiten funcionar a los programas correctamente y
que pueden conducir a la confusión. La figura 26 muestra el diseño final de la
aplicación, a través de la cual se puede acceder a la simulación de cualquier
parte del sistema dando un clic en la parte que interese. Este es un entorno multitarea con simulaciones paralelas e
independientes, cuadros de textos de ayudas interactivas, interfaz de rápido
acceso e intuitiva que integra todos los modelos
Figura 26. Propuesta final de la interfaz gráfica del usuario desarrollada en App Designer Matlab/Simulink.
Fuente: Elaboración propia.
CONCLUSIÓN
Los modelos matemáticos constituyen una herramienta eficaz para analizar y estudiar el comportamiento de sistemas físicos como los presentados en este artículo. A través de ellos se ha podido esclarecer los diferentes interrogantes sobre el comportamiento de sistemas solares aislados operando con cargas en AC como DC.
Mediante el estudio por separado de cada elemento del sistema solar fotovoltaico aislado, se ha profundizado en su comportamiento dinámico. Además, ha permitido el diseño de una herramienta o aplicación parametrizable según las características técnicas de cada elemento del sistema, permitiendo simular sistemas solar fotovoltaicos incorporando datos reales de radicación solar y temperatura del sitio físico donde se realiza el estudio.
Se destaca la importancia de la compresión de las ecuaciones algebro diferenciales que describen el comportamiento de cada dispositivo del sistema, por cuanto esto conduce a la creación de modelos replicables con un nivel de aproximación aceptable con respecto al campo real. Esto se pudo comprobar mediante las pruebas de simulación bajo condiciones STC (paneles solares), pruebas de tiempo de autonomía (baterías) y validaciones mediante cálculos matemático (inversor-carga).
FINANCIAMIENTO
No monetario
AGRADECIMIENTO
A la Universidad Laica Eloy Alfaro de Manabí, Ecuador; por apoyar la investigación.
REFERENCIAS CONSULTADAS
Carmona, D. (2018). Proceso de la energía solar [Solar energy process]. Recuperado de https://n9.cl/e7m1
Cisterna-Arellano, L., Améstica-Rivas, L., & Piderit, M. B. (2020). Proyectos fotovoltaicos en generación distribuida ¿Rentabilidad privada o sustentabilidad ambiental? [Photovoltaic Projects in Distributed Generation. Private Profitability or Environmental Sustainability?]. Revista Politécnica, 45(2), 31-40. https://doi.org/10.33333/rp.vol45n2.03
Cortés-Mura, H, & Peña-Reyes, J. (2015). De la sostenibilidad a la sustentabilidad. Modelo de desarrollo sustentable para su implementación en políticas y proyectos. [From sustainability to sustainability. Sustainable development model for its implementation in policies and projects]. Revista Escuela de Administración de Negocios, (78),40-54.
Cruz, C. (2016). Genes Software - extended and integrated with the R, Matlab and Selegen. Acta Scientiarum. Agronomy, 38(4), 547-552.
Ffrench-Davis, R. (2017). Globalización económica y desarrollo nacional: evolución y algunos desafíos actuales. [Economic globalization and national development: evolution and some current challenges]. Estudios internacionales (Santiago), 49(spe), 89-112.
Inguil-Lema, Á., & Ortega-Espinoza H. (2014). Análisis, modelado y validación de un sistema fotovoltaico para el alumbrado vial de la avenida de las Américas. [Analysis, modeling and validation of a photovoltaic system for street lighting on Avenida de las Américas]. Universidad Politecnica Salesiana sede Cuenca. Recuperado de https://n9.cl/34bv
Kahl, A, Dujardin, J, & Lehning, M. (2019). The bright side of PV production in snow-covered mountains. https://doi.org/10.1073/pnas.1720808116
Lockwood, M., Kuzemko, C., Mitchell, C., & Hoggett, R. (2017). Historical institutionalism and the politics of sustainable energy transitions: A research agenda. Environment and Planning C: Politics and Space, 35(2), 312–333. https://doi.org/10.1177/0263774X16660561
Luna-Merino, M. (2010). Diseño y simulación de inversor monofásico en puente completo modulado mediante PWM para un sistema fotovoltaico. [Design and simulation of a single-phase inverter in full bridge modulated by PWM for a photovoltaic system]. Proyecto de grado. Universidad Carlos III de Madrid. Recuperado de https://n9.cl/5sp3
Marulanda-Durango, J, Ordoñez, J, & Mosquera-Machado, L. (2017). Diseño y construcción de un convertidor dc/dc tipo Boost con PWM ajustable [Design and Construction of a Boost Type DC / DC Converter with Adjustable PWM]. Scientia Et Technica, 22(1),9-14.
Moreno, D. (2017). Desarrollo de un algoritmo en MATLAB para la optimización de la resolución de una tarjeta USRP B210 para aplicaciones SDRadar [Develop of a MATLAB algorithm for the resolutions optimization of an USRP B210 card for SDRadar applications]. Maskay, 7(1), 31-40. https://doi.org/10.24133/maskay.v7i1.338
Muñoz-Vizhñay., J, Rojas-Moncayo, M, & Barreto-Calle, C. (2018). Incentivo a la generación distribuida en el Ecuador. [Incentive pertaining to energy the generation distributed in Ecuador]. Ingenius. Revista de Ciencia y Tecnología, (19), 60-68.
Murillo, D. G. (2003). Modelado y Analisis de sistemas fotovoltaicos [Modeling and Analysis of photovoltaic systems]. Tesis doctoral. Universitat Politécnica de Catalunya. Recuperado de https://n9.cl/2pi95
Ovalle-Cubillos, R. (2014). Sociedad fotovoltaica. [Photovoltaic society]. Ingeniare. Revista chilena de ingeniería, 22(1), 4-5. https://dx.doi.org/10.4067/S0718-33052014000100001
Palella, S. & Martins F. (2015). Metodologia de la investigacion cuantitativa. [Methodology of quantitative research]. Venezuela. FEDEUPEL.
Pereira-Micena, R, Llerena, O., Queiróz-Lamas, W, & Luz-Silveira, J. (2018). Estudio técnico del uso de energía solar y biogás en vehículos eléctricos en Ilhabela-Brasil [A technical study of solar and biogas energy usage in electric vehicles in Ilhabela, Brazil]. Ingenius. Revista de Ciencia y Tecnología, (20), 58-69.
Pérez-Parada, J, Vides-Herrera, C, & Torres-Chávez, I. (2017). Implementación de un sistema fotovoltaico On Grid sobre una estructura de dos ejes controlada, para la promoción de Fuentes no convencionales de Energía Renovables en el Colegio Gonzalo Jiménez Navas de Floridablanca - Santander, Colombia. [The implementation of an On-Grid photovoltaic system on a controlled two-axes structure, for the promotion of non-conventional sources of energy at Gonzalo Jiménez Navas school in Floridablanca- Santander, Colombia]. Revista de Investigación, 41(92), 56-73.
Poznyak, A. S. (2005). Modelado matemático de los Sistemas Mecánicos, Electricos y Electromecánicos [Mathematical modeling of Mechanical, Electrical and Electromechanical Systems]. Internet. Recuperado de https://n9.cl/tazpy
Universidad Laica Eloy Alfaro de Manabí (2020). Datos meteorológicos. [Meteorological data]. Manta- Ecuador.
Vera-Dávila, A, Delgado-Ariza, J, & Sepúlveda-Mora, S. (2018). Validación del modelo matemático de un panel solar empleando la herramienta Simulink de Matlab [Validation of the mathematical model of a solar panel using Matlab/Simulink tool]. Revista de Investigación, Desarrollo e Innovación, 8(2), 343-356. https://dx.doi.org/10.19053/20278306.v8.n2.2018.7972
Vera-Dávila, A., Delgado-Ariza, J., & Sepúlveda-Mora, S. (2018). Validación del modelo matemático de un panel solar empleando la herramienta Simulink de Matlab [Validation of the mathematical model of a solar panel using Matlab's Simulink tool]. REVISTA DE INVESTIGACIÓN, DESARROLLO E INNOVACIÓN, 8(2), 343-356. https://doi.org/10.19053/20278306.v8.n2.2018.7972
©2020 por los autores. Este artículo es de acceso abierto y distribuido según los términos y condiciones de la licencia Creative Commons Atribución-NoComercial-CompartirIgual 4.0 Internacional (CC BY-NC-SA 4.0) (https://creativecommons.org/licenses/by-nc-sa/4.0/).