Se tiene por objetivo realizar un diseño de grafos tipo árbol de expansión a partir de matrices de transporte. Se trabajó con una metodología de proyecto factible, en consideración la teoría de grafos el cual permite establecer la ruta óptima para el transporte. Los datos de la matriz asignada para la resolución del caso práctico, muestra la información de los tiempos de viaje entre zonas de la ciudad de Durán, mismas que han servido de base para el diseño de los árboles de expansión de las zonas uno y dos. Se dividió el área de estudio en catorce zonas, con sus respectivos centroides de mayor generación y atracción de viajes de la población y de esta forma se desarrolló una red una red de transporte que une a todos los nodos de la ciudad de Durán.

Descriptores: Transporte por carretera; vehículo automotor; ingeniería vial. (Tesauro UNESCO).

ABSTRACT

The objective of this work is to design a spanning tree type graph design based on transportation matrices. We worked with a feasible project methodology, taking into consideration the graph theory which allows establishing the optimal route for transportation. The data of the matrix assigned for the resolution of the case study, shows the information of travel times between zones of the city of Durán, which have served as the basis for the design of the spanning trees of zones one and two. The study area was divided into fourteen zones, with their respective centroids of greatest generation and attraction of population trips and in this way a network was developed a transportation network linking all the nodes of the city of Durán.

Descriptors: Road transport; motor vehicles; road engineering. (UNESCO Thesaurus).

INTRODUCCIÓN

De acuerdo con la formación obtenida en el masterado de gestión del transporte con mención en tráfico, movilidad y seguridad vial, se puede mencionar que, a nivel del Ecuador, se han invertido recursos para el desarrollo de proyectos de transporte, muchos de los cuales han servido para asumir las competencias de los Gobiernos Autónomos Descentralizados en el sector estratégico del transporte, tránsito y seguridad vial (Benabent-Fernández-de-Córdoba, 2017). Se ha observado que no todos los proyectos planificados han sido implementados a cabalidad, debido a que las variables que se suelen analizar y sintetizar en los estudios no responden a las necesidades reales que tiene la sociedad para una movilidad sostenible y sustentable, además en muchas ocasiones el personal técnico carece de conocimientos y herramientas fundamentales para la ejecución o resolución de dichos proyectos (Moya-Puente et al. 2017).

Como situación problema se describe que la ciudad Durán, forma parte de la provincia del Guayas, y en la actualidad posee zonas residenciales, comerciales e industriales, su desarrollo económico ha impulsado el crecimiento e implementación de una serie de fábricas y puntos de comercio en sectores estratégicos, motivo por el cual se ha observado el ingreso de varias personas provenientes de otras ciudades del país en busca de empleo y mejores condiciones de vida, impulsando de esta manera el crecimiento poblacional del cantón (Zambrano-Camacho & Orellana-Intriago, 2018).

En la administración del transporte sea público o privado, se ha evidenciado una serie de falencias en la planificación aún con mayor grado de afectación en ciudades pequeñas que carece del equipo humano para gestionar las acciones correspondientes para solucionar dichos inconvenientes (Fernández-de-Córdoba, 2017). Con estos antecedentes y en vista de una falta de políticas locales aplicables al transporte, tránsito y seguridad vial, se ha incrementado del uso del vehículo privado para acceder a los nuevos puntos de comercio e industrias del sector de estudio, lo que conlleva a poseer mayores problemas de congestionamiento del tránsito, especialmente en horas de máxima demanda de la movilidad de personas y bienes de la ciudad (Acosta-Gómez & Acosta-Gómez, 2021).

El presente proyecto para la resolución del caso práctico, más allá de servir como requisito para la obtención de un título de cuarto nivel, busca dar a conocer al lector una herramienta técnica obtenida de la teoría de grafos, para el desarrollo de proyectos de movilidad, tránsito y transporte de ciudades medianas. Se ha planificado establecer un modelo técnico que permita a los usuarios de un sistema de transporte reducir la distancia de los viajes, con lo cual se estima también minimizar los costos, tiempo, entre otras variables cuantitativas para la optimización en redes de transporte.

Dicho de esta manera, con el presente caso práctico se debe proponer una estrategia que permita gestionar los problemas de transporte, por lo cual se plantea una zonificación de la ciudad en 14 zonas de tráfico, con sus respectivos resultados medidos en tiempos de viaje que se muestran en la siguiente tabla. Se pide diseñar el árbol de expansión de las zonas 1 y 2.

Tabla 1.

Matriz de transporte.

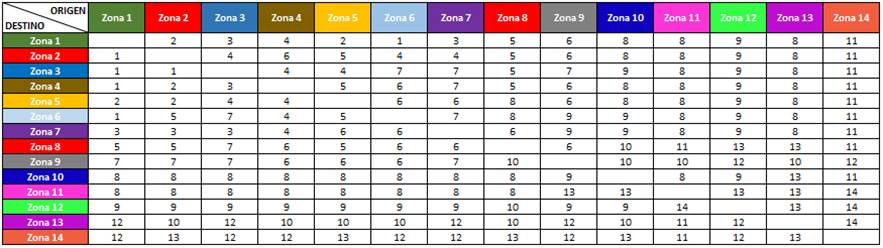
Interfaz de usuario gráfica

Descripción generada automáticamente

Fuente: Los autores.

En consideración el actual trabajo de investigación se ha relacionado con la investigación denominada “selección de rutas en una red de sensor inalámbrica, en base al nivel de batería y distancia entre nodos sensores mediante la utilización del algoritmo de Kruskal” desarrollada por (Mesias, 2016), al ser este un trabajo de gran importancia en el que se planificó una ruta óptima mediante el uso de sensores inalámbricos y modelos matemáticos para disminuir tiempos de viaje, distancias y recursos.

En tal sentido, se tiene por objetivo realizar un diseño de grafos tipo árbol de expansión a partir de matrices de transporte.

Referencial teórico

El proceso de la planificación del transporte a nivel mundial se ha desarrollado a lo largo del tiempo como una especialidad, que ha tenido el propósito de dar facilidades a la apropiada utilización de los diferentes modos de transporte existentes (Ruíz, 2017, p. 3). Según (Arias, 2007), para una mejor planificación del transporte, se requiere disponer de objetivos claros y que se orienten a una serie de etapas, las cuales se resumen a continuación:

a) Recolección de información, en esta primera etapa el planificador recopila todos los datos necesarios para analizar el caso de estudio de transporte.

b) Elaboración de la red, desarrolla de manera gráfica una simulación del sistema de transporte que se encuentra analizando.

c) Construcción del modelo de transporte, en esta etapa intermedia el planificador construye y simula mediante un modelo matemático apropiado la generación, distribución y asignación de los viajes del área de estudio.

d) Previsiones, esta etapa se refiere a visualizar los efectos que puede tener el sistema de transporte, realizar ajustes y los cambios necesarios del modelo.

e) Evaluación de los resultados, en esta etapa el planificador evalúa los resultados obtenidos del estudio y analiza las distintas alternativas que se puedan proponer para el óptimo funcionamiento del sistema de transporte. (Arias, 2007, p. 5)

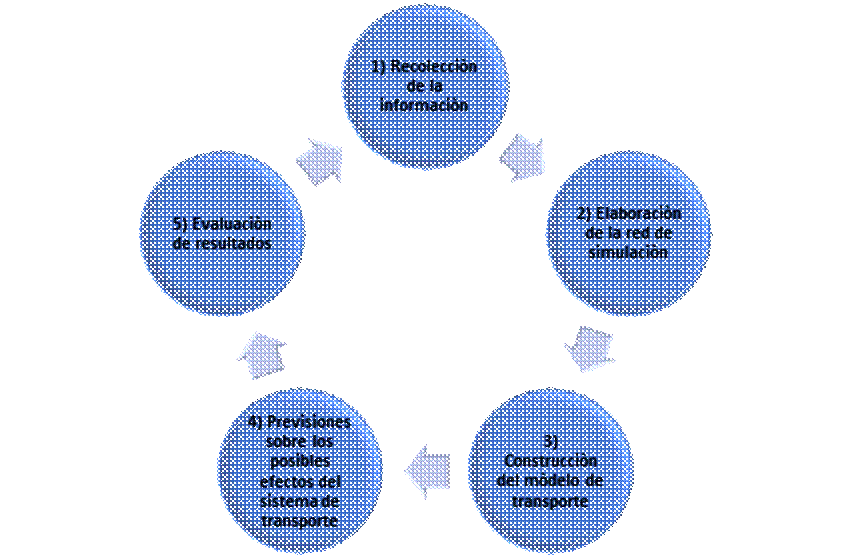
Figura 1. Proceso de planificación del transporte.

Fuente: Arias (2007).

Zonificación del área de estudio

Comprende la división de sectores de un área de estudio denominada “zonas de tráfico” o básicamente “zonas”; en esta división por lo general se realiza de manera geográfica, según el uso de suelo y tomando en consideración datos socioeconómicos de la población, con la finalidad de abarcar los orígenes y destinos de los viajes, cabe mencionar que las zonas pueden ser internas y externas (Arias, 2007, p. 7).

La cantidad y extensión de las zonas dependerá del grado de precisión que se pretenda alcanzar con el estudio, los planificadores deben tomar en consideración, que para la delimitación se analiza la relación costo-beneficio, ya que, a mayor número de zonas de estudio, se requerirá mayor inversión económica y esto se da básicamente por la cantidad de datos que se vaya a sintetizar (Arias, 2007, p. 7).

Para ciudades pequeñas y medianas, los expertos en planificación del transporte sugieren que las zonas se delimiten en áreas donde exista una población que oscile entre los 1.000 a 3.000 habitantes, mientras que para áreas metropolitanas se pueden delimitar a una población comprendida entre 5.000 a 10.000 habitantes. En la zonificación se debe evitar excesos, debido a que una cantidad extensa de zonas generaría que los datos estadísticos resulten no representativos, por su parte una cantidad muy reducida o simplificada de zonas, se obtendrían datos estadísticos poco aceptables para la toma de decisiones. Las formas de las zonas pueden variar, sin embargo, lo recomendable son formas regulares, de tipo rectangulares o circulares en el mejor de los casos (Arias, 2007, p. 7).

Centroide de zona

Es considerado como un punto localizado en el interior de una zona, por medio del cual ingresan y salen los viajes que se generan y se atraen en dicho sector, este centroide por lo general se debe localizar en un espacio determinado donde básicamente se concentre la mayor densidad demográfica y cantidad de actividades de acuerdo con el tipo de uso de suelo, sean estos de carácter residencial, comercial, industrial, entre otras (Arias, 2007, p. 16).

Conectores de centroide

Son líneas imaginarias que suelen unir centroides de una red de transporte, para lo cual es importante definir los nodos de transporte a los que se unirán los conectores; así como también es necesario definir la velocidad promedio de las vías adyacentes al centroide localizado en su respectiva zona (Arias, 2007, p. 16).

Nodos de transporte

Se comprende como nodos logísticos de transporte a los sectores o puntos geográficos estratégicos de una red, donde naturalmente se pueden efectivizar la gestión de flujos de un determinado sistema, estos pueden ser terminales, estaciones, puertos, aeropuertos o lugares generadores o atractores de viajes, sean estos destinados para el trasladar personas o mercancías (Arias, 2007, p. 16).

Matrices origen destino

Una vez definido el área de estudio y haber obtenido los datos necesarios de la oferta y la demanda de transporte, así como también la zonificación, nodos estratégicos, centroides entre otras variables que dependerán del caso de estudio, se procede con la elaboración de la matriz origen-destino, en la cual se representará en el interior de sus celdas todos los viajes que se generan (origen) y se atraen (destino) entre zonas, de acuerdo al medio de transporte terrestre utilizado (Arias, 2007, p. 28). A continuación, se muestra un pequeño ejemplo de matriz origen-destino en la misma se identifica los viajes (T) que se realizan entre los nodos de las diferentes zonas del área de estudio y a la vez se identifica la sumatoria total de los orígenes (On) y destinos (Dn) realizados en la misma.

Tabla 2.

Ejemplar de matriz origen-destino.

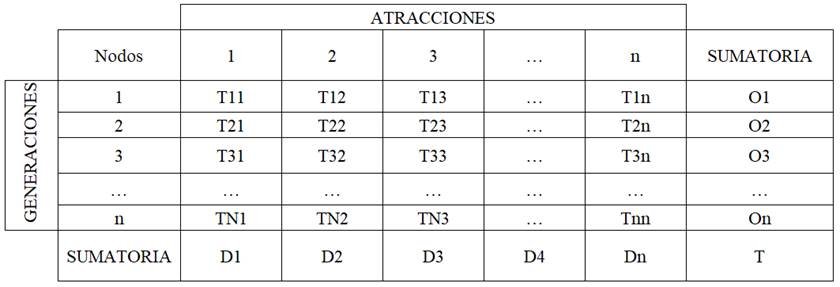
Tabla

Descripción generada automáticamente

Fuente: Arias (2007).

Redes de transporte

Se considera un esquema real del sistema de transporte sobre el cual el planificador analiza y ensaya las diferentes alternativas para su óptimo funcionamiento y que aplicando una asignación apropiada a la red suministra una idea concreta de los volúmenes de tráfico actuales y proyectados, además de costos de operación (Arias, 2007, p. 16). Por ejemplo, las redes pueden estar compuestas por rutas, ramales de los sistemas de transporte existentes que operan en una determinada ciudad y estos sistemas lo pueden integrar varios modos de transporte de bienes o pasajeros.

Árboles y bosques en redes no dirigidas

El grafo de tipo “árbol” es conocido como una gráfica de una red no dirigida de tipo acíclica y conexa, si la gráfica es no dirigida, pero probablemente disconexa a la misma se la denomina como un “bosque”. Dicho de otra manera, el conjunto de grafos que contienen árboles se lo conoce como “bosque”, sin embargo, si en el conjunto de gráficos se observa al menos un ciclo, no se podría considerar a la red ni como “árbol” ni como “bosque” (González, 2006, p. 7).

Gráfico, Gráfico de líneas

Descripción generada automáticamente

Figura 2: Tipo de grafos o gráficos en redes.

Fuente: González (2006).

En la figura anterior se observa un ejemplo sencillo de tres gráficos o grafos en redes no dirigidos, todas tres representadas por once nodos, en la primera se muestra una gráfica de tipo “árbol”, en la segunda un “bosque”, mientras que en la tercera se indica una red con al menos un ciclo entre los nodos uno, dos, cuatro y cinco; por lo tanto, a este último grafo no se lo considera ni “árbol” ni “bosque”.

Árbol enraizado

Según (González, 2006) el “árbol enraizado”, se representa a un grafo que contiene un vértice o nodo distinguido de otros nodos, al primer vértice se le denomina “raíz del árbol” y este puede ser identificado como el padre de los nodos siguientes existentes en la red, también el árbol enraizado puede tener características de grados, profundidad y una altura específica como se muestra a manera de ejemplo en la siguiente ilustración:

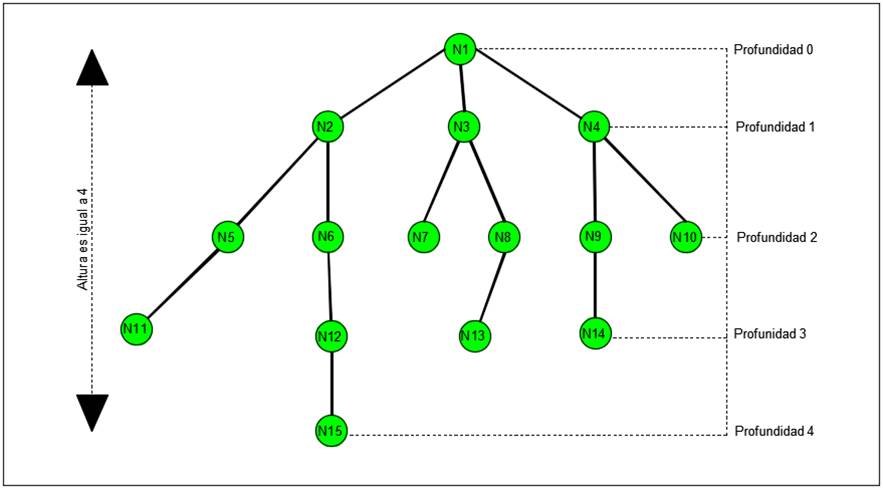
Gráfico, Gráfico de líneas

Descripción generada automáticamente

Figura 3: Ejemplar de árbol enraizado.

Fuente: González (2006).

En el ejemplo anterior se muestra en primer lugar una red no dirigida con un grafo de tipo “árbol enraizado” (Correa-Espinal et al. 2011), que está compuesto por quince nodos o vértices, en segundo lugar, se puede evidenciar que el primer nodo (N1) es el padre de los nodos o vértices (N2), (N3) y (N4) y por último se indica que el grafo posee una profundidad enraizada de cero a cuatro, por lo tanto, su altura es igual a cuatro.

Árbol de expansión mínima

Se conoce como árbol de expansión, aquel árbol cuyo gráfico no dirigido es de tipo acíclico y que conecta a todos los vértices de este, por su parte el grafo de expansión mínima como su nombre ya lo indica es aquel que conecta a todos los vértices o nodos de un grafo bajo un peso mínimo que puede estar traducido en términos de costo, distancia, tiempo u otras variables que se ajustan a las necesidades de un estudio en particular. (González, 2006).

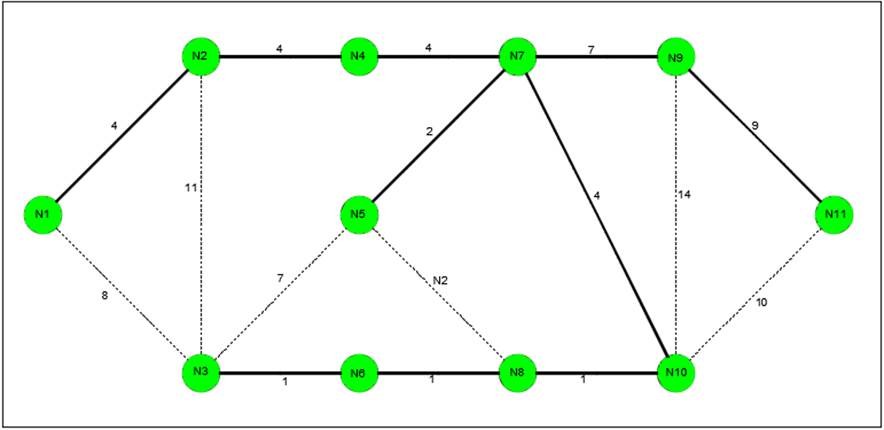
Pantalla de video juego

Descripción generada automáticamente con confianza baja

Figura 4: Ejemplar de Árbol de expansión mínima.

Fuente: González (2006).

La figura anterior muestra en primer lugar una red no dirigida y compuesta por once nodos, mismos que se encuentran enlazados con una cantidad expresada en este caso en términos de costos, a su vez se puede observar que lo remarcado con negrita es un grafo de tipo “árbol de expansión mínima”, ya que cumple con los requisitos para que sea considerado como tal y además une todos los nodos bajo un costo total mínimo de 37.

MÉTODO

Se trabajó con una metodología de proyecto factible, en consideración la teoría de grafos el cual permite establecer la ruta óptima para el transporte, se elaboró los árboles de expansión requeridos de los nodos uno y dos de la matriz de transporte considerando las condiciones que sugieren varios autores. La resolución del caso de estudio de diseño de grafos a partir de matrices de transporte para una ciudad media para efectos de análisis se desarrolló las siguientes etapas: tomando en consideración todos los nodos existentes en la matriz del caso práctico:

FASE 1: Se identificó en primera instancia cada una de las zonas de análisis de la matriz existente, en este caso las zonas 1 y 2 en forma horizontal.

FASE 2: Se procedió a zonificar el área de estudio para efectos del análisis se consideró como “XYZ”, tomando en cuenta todos los nodos existentes del caso práctico, partiendo de la información y nodos de la de la matriz de transporte.

FASE 3: Se analizó el contenido de los tiempos de viajes existentes entre cada uno de los nodos de las zonas de origen y destino.

FASE 4: Con la información anterior, se procedió a graficar el árbol de expansión, tanto para la zona 1 como para la zona 2, tomando en consideración los tiempos de viajes asignados.

RESULTADOS

Para la resolución del presente caso práctico se ha tomado en consideración la información teórica y referencial expuesta en la sección número (02) del presente documento, su desarrollo se evidencia por medio de las siguientes fases:

FASE 1: Se identificó en primera instancia cada una de las zonas de análisis de la matriz existente, en este caso las zonas 1 y 2 en forma horizontal:

Tabla 3.

Matriz de transporte, identificación de los resultados de las zonas 1 y 2.

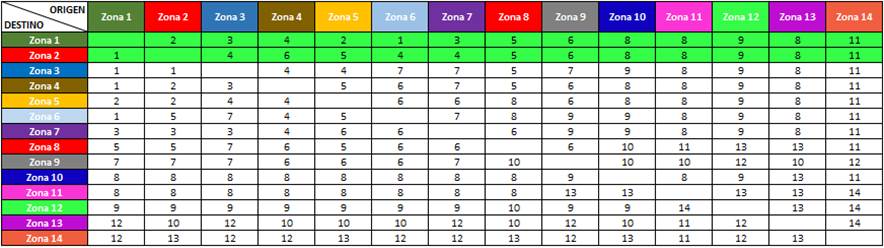
Aplicación, Tabla, Excel

Descripción generada automáticamente

Elaboración: Los autores.

FASE 2: Se procedió a zonificar el área de estudio, partiendo de la información y nodos de la de la matriz de transporte.

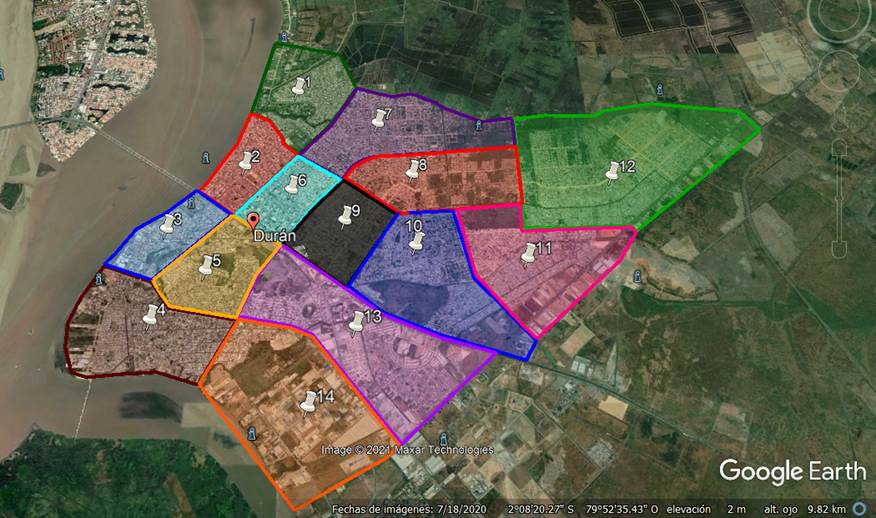
Figura 5: Zonificación del área de estudio.

Fuente: Google Earth. Adaptación de los autores.

FASE 3: Se analizó el contenido de los tiempos de viajes existentes entre cada uno de los nodos de las zonas de origen y destino, tal y como se muestra a continuación. Para la zona 1, se posee los siguientes tiempos de viaje:

Tabla 1.

Tiempos de viaje de la zona 1 a las demás zonas de análisis.

Parámetro	Tiempo
De la zona 1 a la zona 2	2
De la zona 1 a la zona 3	3
De la zona 1 a la zona 4	4
De la zona 1 a la zona 5	2
De la zona 1 a la zona 6	1
De la zona 1 a la zona 7	3
De la zona 1 a la zona 8	5
De la zona 1 a la zona 9	6
De la zona 1 a la zona 10	8
De la zona 1 a la zona 11	8
De la zona 1 a la zona 12	9
De la zona 1 a la zona 13	8
De la zona 1 a la zona 14	11

Elaboración: Los autores.

A continuación, se presenta la distribución de los tiempos de viaje desde la zona 2 hacia las demás zonas de estudio.

Tabla 2.

Tiempos de viaje de la zona 2 hacia las demás zonas de análisis.

Parámetro	Tiempo
De la zona 2 a la zona 1	1
De la zona 2 a la zona 3	4
De la zona 2 a la zona 4	6
De la zona 2 a la zona 5	5
De la zona 2 a la zona 6	4
De la zona 2 a la zona 7	4
De la zona 2 a la zona 8	5
De la zona 2 a la zona 9	6
De la zona 2 a la zona 10	8
De la zona 2 a la zona 11	8
De la zona 2 a la zona 12	9
De la zona 2 a la zona 13	8
De la zona 2 a la zona 14	11

Elaboración: Los autores.

FASE 4: Con la información anterior, se procedió a graficar el árbol de expansión, tanto para la zona 1 como para la zona 2, tomando en consideración los tiempos de viajes asignados.

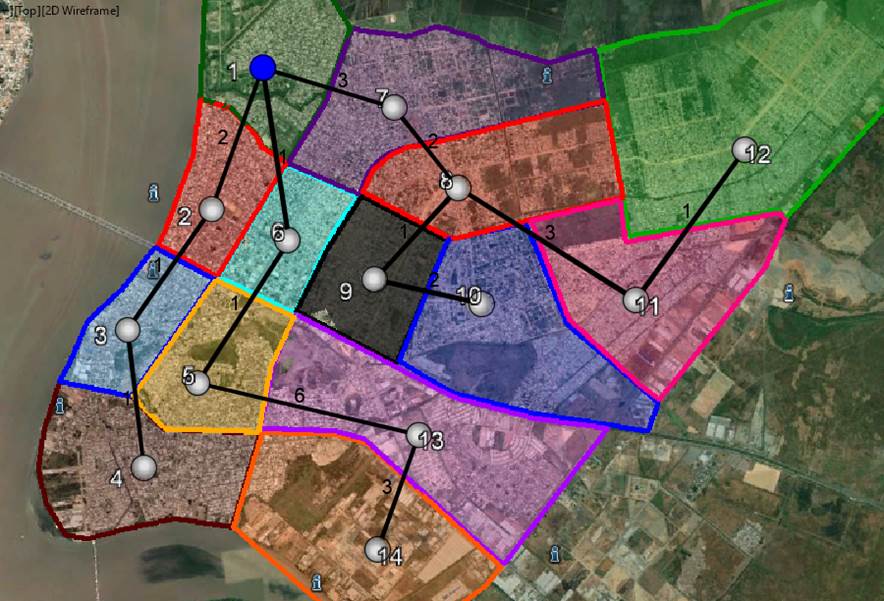
Mapa

Descripción generada automáticamente

Figura 6. Árbol de expansión de la zona 1.

Fuente: Google Earth. Adaptación de los autores.

En la ilustración anterior se muestra el árbol de expansión desde la zona 1, el cual se distribuye hacia las demás zonas de análisis, el mismo que fue trazado en base a todos los tiempos de la matriz de transporte, además se puede evidenciar que el tiempo total de recorrido en este ejemplo desde la zona 1 hacia las diferentes zonas de tránsito es de 27 minutos.

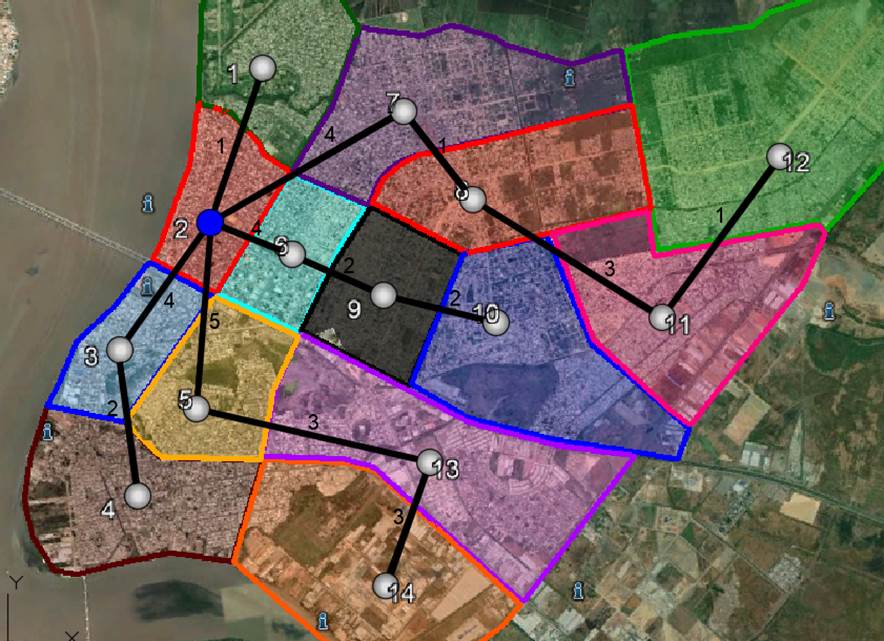
Imagen que contiene Mapa

Descripción generada automáticamente

Figura 7: Árbol de expansión de la zona 2.

Fuente: Google Earth. Adaptación de los autores.

Del mismo modo en la ilustración anterior, se muestra el árbol de expansión desde la zona 2, el cual se expande hacia las demás zonas de tránsito, por lo que se puede evidenciar que el tiempo total de recorrido para este caso desde la zona 2 hacia las diferentes zonas de tránsito es de 35 minutos.

De la zonificación el área de estudio, se determinó 14 zonas de tránsito, que fueron distribuidos en 14 nodos o vértices centrales de cada zona, de tal modo que, mediante el uso de herramientas de georreferenciación, fue posible graficar los árboles de expansión requeridos para la zona 1 y 2 hacia las diferentes zonas de tránsito, teniendo como resultado viajes de 27 y 35 minutos respectivamente.

Con los árboles de expansión graficados para las zonas 1 y 2, se recomienda analizar la implantación de nuevos recorridos de transporte masivo, tales como la reestructuración de rutas del transporte de pasajeros de ámbito intracantonal, así como también la posible implantación de un sistema de transporte alternativo y sostenible, como por ejemplo una ciclovía que se integre a los diferentes modos de transporte regularizados por la autoridad competente de la ciudad.

CONCLUSIONES

Los datos de la matriz asignada para la resolución del caso práctico, muestra la información de los tiempos de viaje entre zonas de la ciudad de Durán, mismas que han servido de base para el diseño de los árboles de expansión de las zonas uno y dos.

Se dividió el área de estudio en catorce zonas, con sus respectivos centroides de mayor generación y atracción de viajes de la población y de esta forma se desarrolló una red una red de transporte que une a todos los nodos de la ciudad de Durán.

De la estructuración de los árboles de expansión, se tomó en consideración los tiempos de viaje mínimos de las zonas uno y dos hacia las diferentes zonas del área de estudio, por lo que se propuso como alternativa de solución de prefactibilidad la implementación de una red de ciclovía o a su vez de acuerdo a un análisis técnico más profundo, que tome en consideración los datos de la demanda de transporte y la oferta existente, este último como por ejemplo la infraestructura vial, sea posible la creación de una ruta de transporte de pasajeros en autobuses, con el propósito de que la población pueda utilizar este servicio y satisfacer sus necesidades de movilidad.

FINANCIAMIENTO

No monetario.

AGRADECIMIENTO

A la Universidad Internacional del Ecuador; por motivar el desarrollo de la investigación.

REFERENCIAS CONSULTADAS

Acosta-Gómez, D., & Acosta-Gómez, C. (2021). Análisis de la situación financiera de los transportistas de carga pesada por el Covid-19, en el cantón Sigchos [ Analysis of the financial situation of heavy cargo transporters due to Covid-19, in the Sigchos cantón]. REVISTA CIENTÍFICA ECOCIENCIA, 8, 225–236. https://doi.org/10.21855/ecociencia.80.646

Arias, C. (2007). Planificación del Transporte [Transportation Planning]. Ed. A&V. Quito.

Benabent-Fernández-de-Córdoba, M. (2017). El transporte público terrestre y la accesibilidad, instrumentos para el análisis funcional del sistema de asentamientos: el caso de Ecuador [Ground public transport and accessibility, instruments for the functional analysis of the settlements system: the case of Ecuador]. Estoa. Revista de la Facultad de Arquitectura y Urbanismo de la Universidad de Cuenca, 6(11), 99-122. https://doi.org/10.18537/est.v006.n011.a06

Correa-Espinal, A, Cogollo Flórez, J, & Salazar López, J. (2011). Aplicación de la teoría de grafos en la solución de problemas con impacto ambiental [Application of the graph theory on the solution of environmental problems]. Producción + Limpia, 6(1), 9-20.

Fernández-de-Córdoba, M. B. (2017). El transporte público terrestre y la accesibilidad, instrumentos para el análisis funcional del sistema de asentamientos: el caso de Ecuador [Land public transportation and accessibility, tools for the functional analysis of the settlement system: the case of Ecuador]. Estoa. Revista De La Facultad De Arquitectura Y Urbanismo De La Universidad De Cuenca, 6(11), 83–97. https://doi.org/10.18537/est.v006.n011.a06

González, J. (2006). Algoritmos en gráficas: arboles de expansión mínima y caminos cortos [Algorithms on graphs: minimum spanning trees and shortest paths]. Ed. Instituto Politecnico Nacional. México D.F.

Mesias, D. (2016). Selección de rutas en una red de sensor inalámbrica, en base al nivel de batería y distancia entre nodos sensores mediante la utilización del algoritmo de kruskal [Route selection in a wireless sensor network based on battery level and distance between sensor nodes using the kruskal algorithm.]. Recuperado desde https://cutt.ly/OFnMech

Moya-Puente, M, Carrillo Gurumendi, O, & Huerta Cruz, S. (2017). Análisis del nivel de satisfacción de los usuarios del sistema integrado transporte masivo urbano de Guayaquil metrovía, 2016 [Analysis of the level of satisfaction of users of the integrated urban mass transit system of Guayaquil Metrovía, 2016.]. Revista Universidad y Sociedad, 9(2), 147-155

Ruíz, S. (2017). Modelacion de una red de transporte universitaria mediante el software VISUM 15 [Modeling of a university transport network using VISUM 15 software]. Recuperado desde http://hdl.handle.net/20.500.12404/9257

Zambrano-Camacho, N, & Orellana-Intriago, C. (2018). Factores que influyen en la calidad del servicio de transporte pesado en Guayaquil [Factors that influence the quality of the heavy transportation service in Guayaquil]. Revista Universidad y Sociedad, 10(5), 224-231.

©2022 por los autores. Este artículo es de acceso abierto y distribuido según los términos y condiciones de la licencia Creative Commons Atribución-NoComercial-CompartirIgual 4.0 Internacional (CC BY-NC-SA 4.0) (https://creativecommons.org/licenses/by-nc-sa/4.0/).