http://dx.doi.org/10.35381/r.k.v5i2.1013

Predicción del rendimiento de cultivos agrícolas usando aprendizaje automático

Agricultural Crop Yield Prediction Using Machine Learning

Joel Junior García-Arteaga

jgarcia5169@utm.edu.ec

Universidad Técnica de Manabí, Portoviejo

Ecuador

https://orcid.org/0000-0002-9261-5066

Jesús Javier Zambrano-Zambrano

jzambrano1217@utm.edu.ec

Universidad Técnica de Manabí, Portoviejo

Ecuador

https://orcid.org/0000-0001-8986-1832

Roberth Alcivar-Cevallos

roberth.alcivar@utm.edu.ec

Universidad Técnica de Manabí, Portoviejo

Ecuador

https://orcid.org/0000-0001-6282-8493

Walter Daniel Zambrano-Romero

walter.zambrano@utm.edu.ec

Universidad Técnica de Manabí, Portoviejo

Ecuador

https://orcid.org/0000-0002-0225-3955

Recepción: 05 de  julio 2020

Revisado: 28 de agosto 2020

Aprobación: 17 de septiembre 2020

Publicación: 01 de octubre 2020

RESUMEN

Se aborda la predicción del rendimiento de los cultivos a través del aprendizaje automático. Se usaron dos variables predictoras: hectáreas cosechadas, y producción en toneladas. Para el primer caso, el mejor modelo fue una arquitectura de red neuronal densa (DNN), con un MSE de 0.0081, seguido de los Random Forest (RF) con un MSE de 0.0104, árboles de decisión (AD) con 0.0168, y finalmente las máquinas de soporte vectorial (SVM) con 0.0328. Cuando se predijo producción en toneladas, el mejor modelo fue el de los RF con un MSE de 0.0550, seguidos de AD con 0.1418, DNN con 0.1489, y finalmente SVM con 0.3420. El test estadístico de diferencia significativa mostró que no existe tal diferencia entre el rendimiento de los modelos cuando se predice la variable hectáreas cosechadas, pero si para el caso de producción en toneladas, donde la capacidad predictiva de RF fue de 95% aproximadamente.

Descriptores: Agricultura; investigación agrícola; inteligencia artificial. (Palabras tomadas del Tesauro UNESCO).

ABSTRACT

Crop yield prediction is addressed through machine learning. Two predictor variables were used: hectares harvested, and production in tons. For the first case, the best model was a dense neural network (DNN) architecture, with a MSE of 0.0081, followed by Random Forest (RF) with an MSE of 0.0104, decision trees (AD) with 0.0168, and finally vector support machines (SVM) with 0.0328. When production in tons was predicted, the best model was RF with a MSE of 0.0550, followed by AD with 0.1418, DNN with 0.1489, and finally SVM with 0.3420. The statistical test of significant difference showed that there is no such difference between the performance of the models when the variable hectares harvested is predicted, but in the case of production in tons, where the predictive capacity of RF was approximately 95%.

Descriptors: Agriculture; agricultural research; artificial intelligence. (Words taken from the UNESCO Thesaurus).

INTRODUCCIÓN

En el campo de la agricultura, se realizan muchos procesos que hoy en día son automatizados, en los que permiten entre varias cosas, regular, controlar y administrar de una manera aceptable los recursos que en un cultivo se requiere para una buena producción, mediante dispositivos como sensores, actuadores, que, comunicados entre sí deben operar de cierta manera para optimizar entre varios aspectos: tiempo, dinero y mano de obra (Herrara-Díaz, 2016). Una de las consecuencias más importantes de esta modernización agraria es que aumenta considerablemente la integración de la agricultura con el resto de la economía, tanto a nivel de cada país como a nivel mundial. El sistema productivo de la agricultura moderna está mucho más relacionado con todos los aspectos económicos y, por lo tanto, su evolución está vinculada, de forma creciente, a la dinámica económica general (Food and Agriculture Organization, FAO, 2002). 

Es por este vínculo entre economía y agricultura, que resulta imprescindible lograr un buen rendimiento en los cultivos. Predecir los niveles de producción en Sudamérica puede ser muchas veces una tarea desafiante, puesto que es una región cuya agricultura es altamente sensible a los cambios climáticos, sobre todo a las ondas de frío y de calor, mismas que afectan directamente a la producción y seguridad de los alimentos de la región. Estos cambios climatológicos pueden afectar la producción de cultivos a largo plazo, pero también lo hace a corto plazo, aumentando costos repentinamente y afectando sobre todo a regiones con bajos ingresos económicos. Sudamérica será la región clave en cuanto a producción agrícola se refiere en el futuro, por lo que uno de los mayores retos que se tiene es ser capaz de optimizar la producción de cultivos (Marengo et al., 2014).

Realizar tareas de predicción, por otro lado, no es una tarea para nada sencilla, por cuanto en productos como la caña de azúcar, se necesita la evaluación de múltiples factores, muchas veces impredecibles, como lo es el clima. Esto hace que los agricultores tengan la difícil tarea de tomar decisiones de cómo sembrar; si sembrar poco, mucho, o en el peor de los casos, no sembrar nada. La complejidad de evaluar estos factores hace que la decisión tomada por parte de los agricultores no siempre sea la mejor, ocasionando grandes pérdidas monetarias (Laurentin, 2020). 

En la literatura es posible encontrar varios estudios (Carrillo & Parraga-Alava, 2018; Parraga-Alava, et al., 2020), donde se han aplicado algoritmos de aprendizaje automático para tareas de clasificación/predicción. En el caso de predicción de cultivos, (Crane-Droesch, 2018), analizó el rendimiento del maíz en el medio oeste de Estados Unidos, aplicando un modelado que utiliza una variable semi paramétrica de una red neuronal profunda, para de esta manera ser capaces de capturar la no linealidad de los datos. El enfoque de este estudio, al igual que (Khaki & Wang, 2019), se centró en ser capaz de tratar con el problema de la alta dimensionalidad de los datos, y ser capaces de capturar gran parte de la no linealidad de estos.

 El enfoque adoptado por (Khaki & Wang, 2019), consistió en el uso de dos redes neuronales profundas para predecir la producción, superó a otros modelos populares como Lasso, redes neuronales superficiales (SNN) y árboles de decisión. Este estudio reveló que los factores ambientales tienen un fuerte impacto sobre el rendimiento de los cultivos, siendo un factor más determinando que, por ejemplo, el genotipo de las plantas. Finalmente, (Van Klompenburg et al., 2020), analizó los métodos y características más utilizados, acerca de la problemática de la alta dimensionalidad que tienen los conjuntos de datos utilizados para predicción de producción en cultivos agrícolas. 

La mayor parte de los estudios realizados pertenecen a regiones de Estados Unidos y Europa, y si bien en Sudamérica también se han hecho estudios acerca de la producción de cultivos, en su gran mayoría están basados en analizar cómo ha sido la producción a lo largo del tiempo, mas no en predecir. Por ejemplo, (Ferrero et al., 2018), analiza la producción en términos de estabilidad con respecto al cambio climático, viendo qué factores son los que más afectan a los cultivos.

Por otro lado, (Seo & Mendelsohn, 2008), presentaron un enfoque similar, pero esta vez centrándose en analizar las decisiones tomadas por parte de los agricultores cuando el cambio climático afectó sus cultivos. Estos estudios están centrados en el proceso de descripción de cómo ciertos factores del cambio climático han afectado al rendimiento de cultivos en Sudamérica, asimismo, analizan las decisiones tomadas por los agricultores frente al cambio climático. Es por esta razón, y dado a que Sudamérica es una región con un papel importante en la economía futura (Ferrero, et al., 2018), que surge la necesidad de crear modelos predictivos que ayuden a los agricultores a realizar mejores estimaciones sobre el rendimiento de los cultivos, y de esta forma, minimizar las pérdidas económicas que pueden surgir de una mala cosecha. 

En este artículo se analizan diversos modelos de aprendizaje automático para predecir el rendimiento de los cultivos agrícolas en Argentina. La idea es, a partir de estos modelos, capturar mejor la no linealidad de los datos, y de esta manera, ofrecer predicciones más precisas que permitan tomar mejores decisiones por parte de los agricultores en cuanto a qué cantidad de cierto producto sembrar, teniendo en cuenta el posible rendimiento que este dará.

MATERIALES Y MÉTODOS

Selección de datos

Para la creación del conjunto de datos se recopilaron datos de diversas fuentes. El conjunto de datos principal (obtenido del repositorio de datos del gobierno de Argentina: https://bit.ly/33owdbK) contiene datos acerca de los productos sembrados y cosechados en Argentina desde la campaña de 1969/1970 hasta 2019/2020. Este conjunto de datos se enriqueció con datos referentes al clima (https://bit.ly/3mfDKkt), obtenidos desde el mismo repositorio del gobierno argentino; y con datos geográficos obtenidos del Centro de Información Agroclimática de Argentina (https://bit.ly/36eutnr).

Para el conjunto de datos usado en los experimentos computacionales, se seleccionaron cinco variables climáticas, entre las cuales figuran: velocidad del viento, precipitación, temperatura promedio, máxima y mínima; tres variables de las condiciones geográficas: latitud, longitud, y superficie por encima del nivel del mar; cinco variables del cultivo como tal, entre las que se encuentran: hectáreas sembradas, hectáreas cosechadas, producción y rendimiento. Note que no se consideraron variables genéticas de las plantas, puesto que en \cite{Khaki2019} se demostró que los factores genéticos no afectan tanto como los climáticos; asimismo, \cite{seo2008analysis} llegó a la conclusión de que dos de los factores que más afectan la producción de cultivos son la temperatura y la precipitación, mismas variables que hemos considerado nuestro conjunto de datos. 

En total se seleccionaron 13 variables del conjunto de datos, de las cuales 2 se trataron como variables dependientes (superficie cosechada, producción), y las otras 10 como variables independientes. Las variables dependientes se usan para la predicción del rendimiento de cultivos. Una descripción del conjunto de datos se muestra en la tabla 1.

Tabla 1.

Variables del conjunto de datos utilizado.

Variable	Tipo de dato	Descripción
Lat	Continuo	Latitud del cultivo
Lon	Continuo	Longitud del cultivo
Asnm	Continuo	Altura sobre el nivel del mar medida en metros
Temperatura	Continuo	Temperatura anual promedio medida en °c
Temperatura máxima	Continuo	Temperatura anual máxima medida en °c
Temperatura mínima	Continuo	Temperatura anual mínima medida en °c
Velocidad del viento	Continuo	Medida en km/h (promedio anual)
Cultivo	Categórico	Medida en milímetros de agua (promedio anual)
Precipitación	Entero	Nombre del cultivo a sembrar
Sup. Sembrada	Entero	Hectáreas de tierra sembrada
Sup. Cosechada	Entero	Hectáreas de tierra cosechada
Producción	Entero	Toneladas producida por la cosecha
Rendimiento	Entero	Kilogramos cosechados por hectárea

Preprocesado

Algunos datos pertenecientes a las variables de temperatura, velocidad del viento, y precipitación estaban faltantes, por lo que se completaron usando la media de los que si estaban disponibles. Para evitar que un producto tuviera más peso que el resto, se usó el método de One Hot Encoding. Las variables pasaron un proceso de estandarización, que consiste en aproximar una dimensión a una distribución normal estándar, mediante el uso de la ecuación 1.

(1)

Donde es el tensor de la dimensión estandarizada, es el tensor a estandarizar,  es la media de la dimensión, y finalmente hace referencia a la desviación estándar de la dimensión en cuestión. En este contexto,  hace referencia a la variable a estandarizar, y representa cualquier variable numérica del conjunto de datos.

Modelado

Para predecir el rendimiento de los cultivos se modelaron soluciones usando los métodos de aprendizaje automático: redes neuronales profundas (DNN), máquinas de soporte vectorial (SVM), random forest (RF), y árboles de decisión (AD), debido a que son métodos bastante robustos capaces de capturar no linealidad en datos. Para cada uno de estos modelos se configuran para evaluación una serie de parámetros que se probarán mediante el método de grid search, a excepción de las redes neuronales, puesto que cada arquitectura debe ser diseñada y evaluada individualmente. En la tabla 2 se muestran los parámetros a considerar y sus respectivos valores para cada modelo. 

Tabla 2.

Parámetro a considerar en los experimentos para cada modelo de aprendizaje automático.

Modelo	Parámetro	Valor a evaluar
Random Forest	Bootstrap	Activo,Inactivo
	Estimadores	100, 200, 500
	Criterio	MSE, MAE
Árboles de decisión	Profundidad	10, 15, 20
	Splitter	Random, Best
	Criterio	MSE, FMSE, MAE
SVM	C	0.01, 0.1, 1, 10
	Gamma	0.1, 1, 10
	Kernel	RBF, Linear
DNN	Capas ocultas	1, 3, 4, 8
	Funciones de activación	ReLU, Swish, Elu, Linear
	Épocas	100, 250, 500
	Batch size	250, 500

Validación

Para la fase de entrenamiento se usará el 70% de los datos disponibles, y se dejará el otro 30\% para validar la capacidad de generalización alcanzada por los modelos. Para ello, se consideran las métricas error cuadrático medio (MSE) y coeficiente de determinación (R²). Para probar la capacidad de generalización real de cada modelo, realiza un segundo proceso de validación, en el cual cada modelo se entrena 30 veces, cada una, con una distribución distinta en las variables de entrenamiento, en todos los casos se garantiza la reproducibilidad de los experimentos mediante el uso de semilla.

El MSE (ecuación 2) en este contexto indicará qué tan bien se ajustan los hiperplanos creados por cada modelo al conjunto de datos usado en la etapa de entrenamiento, este métrica se define en la ecuación anterior, donde n es el número de registros disponibles para validación, y_i  hace referencia al valor real para el registro i-ésimo, y la variable  es el valor predicho por el modelo de aprendizaje automático.

(2)

El coeficiente de determinación R² (ecuación 3) ayuda a ver qué tan bueno es un modelo en términos de cuánta varianza logra capturar, algo de suma utilidad puesto que la variable de producción cuenta con datos muy dispersos. El coeficiente de determinación se define mediante la siguiente ecuación tensorial, donde  hace referencia al tensor de valores reales para una variable predictora, es el tensor de valores predichos por el modelo, y por último,  es un escalar que representa la media del tensor de valores reales de una variable predictora. 

(3)

Note que en la ecuación 2 y 3 la variable  hace referencia al valor real de una de las variables predictoras (hectáreas cosechadas o producción), mientras que  se refiere a la predicción hecha por el modelo para una de estas variables. 

RESULTADOS Y DISCUSIÓN

Selección de datos

Los cuatro modelos de aprendizaje automático fueron implementados en Python usando las librerías scikit-learn y keras. El conjunto de datos después de pasar por el proceso de One Hot Encoding escaló de 13 variables a 44, con un total de 83247 registros, de los cuales 58272 se usaron para entrenar los modelos y 24975 para validar su rendimiento.

En la figura 1 se muestra la correlación existente entre las diferentes variables del conjunto de datos usado. En esta se observa que las variables predictoras (sup_cosechada, produccion) tienen una correlación muy baja con las variables independientes, a excepción de las variables de sup\_cosechada con sup_sembrada que tienen una correlación de alrededor de 95%. 

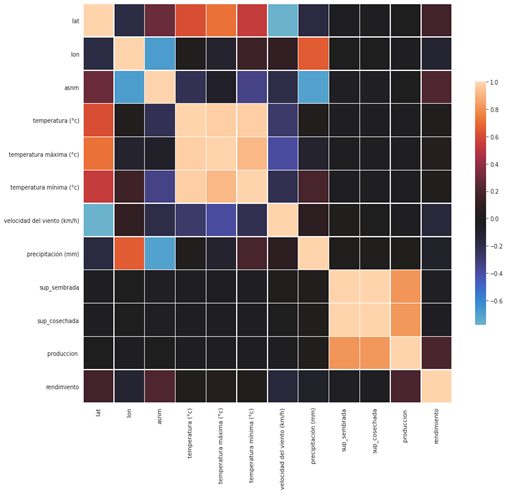
Figura 1.  Correlación entre las variables empleadas en el conjunto de datos.

La poca cantidad de variables correlacionadas dificultó el rendimiento de modelos a la hora de aprender a generalizar la variable producción.   La distribución de la precipitación es otra de las variables, en este caso, independiente, que dificultó el modelado debido a que sus registros estuvieron bastante dispersos. Como se muestra en la figura 2, si bien una gran parte de los datos se encuentran entre 950 y 1250 mm, hay una cantidad de datos considerable que cae por debajo y por encima de este este rango, sin seguir una distribución uniforme. 

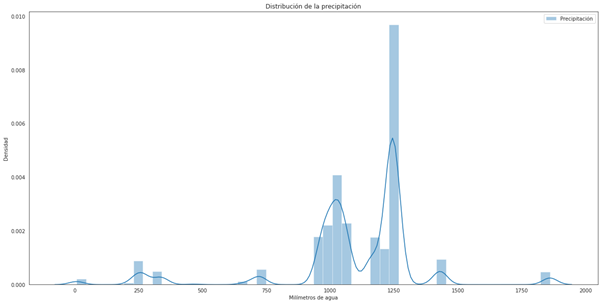
Figura 2.  Distribución de valores de la variable precipitación (mm).

Rendimiento de los modelos

Cada uno de los modelos, a excepción de las redes neuronales (DNN), fue usado junto al método de la grid search, para que este encontrara los mejores parámetros en cada caso. Cada modelo fue valido usando el método de k-Fold con k=5. Los mejores parámetros para cada modelo de acuerdo a la grid search se muestran en la tabla 3.

Tabla 3.

Mejores parámetros obtenidos por la grid search para cada uno de los modelos considerados en la experimentación.

Modelo	Parámetro	Valor para y=cosecha	Valor para y=produccion
Random Forest	Bootstrap	Activo	Activo
	Estimadores	100	200
	Criterio	MSE	MSE
Árboles de decisión	Profundidad	10	15
	Splitter	Random	Random
	Criterio	MSE	FMSE
SVM	C	10	10
	Gamma	1	1
	Kernel	RBF	RBF
DNN	Capas ocultas	3	3
	Funciones de activación	ReLY, swish, elu	ReLY, swish, elu
	Épocas	250	250
	Batch size	250	500

En cuanto al rendimiento, como se muestra en la tabla 4, todos a excepción de los Random Forest tuvieron problemas con la variable produccion, dando un MSE superior a 0.1, que, aunque no es un mal resultado debido a que significa que la distancia entre el hiperplano generado por el modelo y los datos es bastante pequeña, pero como se puede apreciar, el coeficiente de determinación no es tan alto. Y en la SVM esta métrica indica que el modelo no fue capaz de capturar toda la varianza presente en el conjunto de datos. El modelo de Random Forest (RF) fue el modelo con los mejores resultados, aunque en la variable de hectáreas cosechadas fue superado por las redes neuronales profundas (DNN) en la métrica de MSE, este capturó mucha más varianza, llegando al 99% de captura comparado con solo el 82% que logró capturar la red neuronal.

Tabla 4.

Rendimiento de los modelos en el conjunto de validación cuando la variable a predecir es cosecha (hectáreas cosechadas).

Modelo	MSE	R2	Tiempo de ejecución
Random Forest	0.0197	0.9812	0.9 segundos
Árboles de decisión	0.0101	0.9903	37 segundos
SVM	0.0328	0.9688	6 minutos
DNN	0.0081	0.8200	5 minutos

En la tabla 5 se muestra el rendimiento obtenido por cada modelo para la variable de hectáreas cosechadas (sup_cosecha). Aquí se puede apreciar que el mejor modelo fue el de Random Forest (RF), ya que, a pesar de que las redes neuronales (DNN) obtuvieron un MSE menor, el R² indica que que estas no lograron capturar tanta varianza en comparación con los Random Forest (RF). 

Tabla 5.

Rendimiento de los modelos en el conjunto de validación cuando la variable a predecir es producción (produccion).

Modelo	MSE	R2	Tiempo de ejecución
Random Forest	0.1164	0.8913	0.8 segundos
Árboles de decisión	0.0536	0.9493	1.5 minutos
SVM	0.3420	0.6805	6 minutos
DNN	0.1489	0.8609	5 minutos

En la tabla 5 nuevamente se observa que el mejor modelo es el de Random Forest (RF), obtuviendo un MSE bastante bajo en comparación con los demás modelos, y obtuviendo un R² bastante alto, indicando que logró capturar gran parte de la varianza en los datos.

El modelo  Random Forest (RF) al ser el que mejores resultados obtuvo, se sometió a un segundo proceso de validación, donde fue entrenado 30 veces y para cada una de ellas se capturó el MSE y R²  promedios, así como la desviación estándar obtenida en cada métrica. Para la variable producción, promedio de MSE obtenido por el modelo fue de 0.085670, con una varianza de 0.0529, lo que en principio indicaría que el modelo realmente ha logrado converger en un punto donde fue capaz de capturar gran parte de la no linealidad de los datos.

En cuanto al R², obtuvo una media de 0.9189 y una desviación estándar de 0.0434, confirmando que el modelo representa bastante bien la dispersión del conjunto de datos, esto en cuanto a la variable de producción. Para la variable de hectáreas cosechadas, se obtuvo un MSE de 0.0145 con una desviación estándar de 0.0053. El R² fue de 0.9863 y una desviación estándar de 0.0049. Al igual que para la variable de producción, el modelo logró converger en un error bastante bajo y logró representar la dispersión de datos que ocurre en el conjunto de datos. 

Para medir si existe una diferencia significativa en los resultados obtenidos entre los modelos evaluados se utilizó al test ANOVA, con una hipótesis nula H0 que establece que no existe una diferencia significativa entre el MSE promedio o R² promedio de los grupos, y una hipótesis alterna H1 que establece que existe una diferencia significativa entre el rendimiento de los grupos. Para ello se usaron los datos obtenidos de los modelos probados en la tabla 4-5 sobre quince ejecuciones para cada variable predictora. Cuando la la variable a predecir era hectáreas cosechadas (sup_cosechada) se obtuvo un p-value de 0.3050 para MSE, y 0.3042 para R², superando el nivel de significación de 0.05, por lo que concluye que no existe una diferencia significativa entre el rendimiento de los modelos testeados. Por otro lado, cuando la variable a predecir fue la producción en toneladas (produccion) se obtuvo un p-value de 1.28x10^-23 para R2 y 7.251x10^-19 para MSE, un resultado mucho menor que el nivel de significación de 0.05, por lo que se rechaza la hipótesis nula, y se concluye que existe una diferencia significativa entre los modelos evaluados.

CONCLUSIONES

En este trabajo se utilizaron modelos de aprendizaje automático para proponer soluciones en lo que respecta a la predicción del rendimiento de cultivos, dando resultados muy parecidos a estudios realizados que abarcan esta temática. El enfoque utilizado consideró algoritmos predictores conocidos como redes neuronales profundas (DNN), máquinas de soporte vectorial, árboles de decisión (AD) y Random Forest (RF) que fueron entrenamos para realizar la predicción considerando variables climáticas, de cultivo y condiciones geográficas

De estos modelos de aprendizaje automático fue el Random Forest (RF), el que logró obtener mejores resultados, con un MSE de 0.0101 y un R² de 0.9903 para la variable de hectáreas cosechadas, y un MSE de 0.0536 con un R² de 0.9493 para la variable de producción. A este modelo le siguieron los árboles de decisión (AD) con 0.0197 de MSE y 0.9812 en el R² para la variable de hectáreas cosechadas, y para la variable de producción obtuvo un MSE de 0.1164 y un R² de 0.8913.

Las pruebas estadísticas evidenciaron que existe diferencia significativa entre el rendimiento de los modelos cuando se predice la variable producción en toneladas, en cuyo caso, el modelo basado en Random Forest (RF) tuvo mejor capacidad predictiva al lograr capturar patrones complejos entre variables con muy poca correlación, y con menos capacidad de cómputo que los otros modelos considerados en el estudio.  Por lo que este es el modelo que debe ser usado para realizar predicciones relacionados a los datos en estudio.

Para trabajos futuros se puede optar por la creación de modelos capaces de predecir los cambios climáticos que podrían suceder durante el periodo que dura la cosecha y que podrían afectar negativamente su rendimiento, siendo estos capaces de predecir posibles perturbaciones climáticas, que puedan llegar a presentarse. Además de que se podría expandir el área de muestreo, abarcando más países de Sudamérica.

FINANCIAMIENTO

No monetario

AGRADECIMIENTO

A la Universidad Técnica de Manabí, Portoviejo; por motivar el desarrollo de la investigación.

REFERENCIAS CONSULTADAS

Carrillo, J.M., Parraga-Alava, J. (2018). How Predicting The Academic Success of Students of the ESPAM MFL? A Preliminary Decision Trees Based Study. 2018 IEEE Third Ecuador Technical Chapters Meeting (ETCM), Cuenca, 2018, pp. 1-6. https://doi.org/10.1109/ETCM.2018.8580296

Crane-Droesch, A. (2018). Machine learning methods for crop yield prediction andclimate change impact assessment in agriculture. Environmental Research Letters, 13(11); 1-12. https://doi.org/10.1088/1748-9326/aae159

Ferrero, R., Lima, M. & Gonzalez‐Andujar, J. (2018), Crop production structure and stability under climate change in South America. Ann Appl Biol, 172: 65-73. https://doi.org/10.1111/aab.12402

Food and Agriculture Organization, FAO. (2002). Agricultura mundial: hacia los años 2015/2030 [World agriculture: towards the years 2015/2030]. Technical Report 1. Recuperado de https://n9.cl/n29i7

Herrera-Díaz, C. A. (2016). Implementación de un módulo de análisis estadístico y predictivo para agricultura utilizando bigdata y machine learning, integrado al sistema Iotmach. [Implementation of a statistical and predictive analysis module for agriculture using bigdata and machine learning, integrated to the Iotmach system]. Trabajo de titulación. Carrera de ingeniería de sistemas. Universidad Técnica de Machala. Recuperado de https://n9.cl/abp1

Khaki, S. & Wang, L. (2019). Crop Yield Prediction Using Deep Neural Networks. Plant Sci. 10:621. https://doi.org/10.3389/fpls.2019.00621

Laurentin, H. (2020). Importancia de la predicción del rendimiento en caña de azúcar en un contexto de transformación digital. SofOS. Recuperado de https://n9.cl/fl2vh

Marengo JA, Chou SC, Torres RR, Giarolla A, Alves LM, Lyra A. (2014). Climate change in Central and South America: Recent trends, future projections, and impacts on regional agriculture. CCAFS Working Paper no. 73. Copenhagen, Denmark: CGIAR Research Program on Climate Change, Agriculture and Food Security (CCAFS). https://hdl.handle.net/10568/41912

Parraga-Alava J., Alcivar-Cevallos R., Riascos J.A., Becerra M.A. (2020) Aphids Detection on Lemons Leaf Image Using Convolutional Neural Networks. In: Botto-Tobar M., Zamora W., Larrea Plúa J., Bazurto Roldan J., Santamaría Philco A. (eds) Systems and Information Sciences. ICCIS 2020. Advances in Intelligent Systems and Computing, vol 1273. Springer, Cham. https://doi.org/10.1007/978-3-030-59194-6_2

Seo, S. N. & Mendelsohn, R. (2008). An analysis of crop choice: Adapting to climate change in South American farms. Ecological economics, 67(1):109–116. https://doi.org/10.1016/j.ecolecon.2007.12.007

Van Klompenburg, T., Kassahun, A., & Catal, C. (2020). Crop yield prediction using machine learning: A systematic literature review. Computers and Electronics in Agriculture, 177. https://doi.org/10.1016/j.compag.2020.105709

©2020 por los autores. Este artículo es de acceso abierto y distribuido según los términos y condiciones de la licencia Creative Commons Atribución-NoComercial-CompartirIgual 4.0 Internacional (CC BY-NC-SA 4.0) (https://creativecommons.org/licenses/by-nc-sa/4.0/).